��Ŀ����
����Ŀ��һ��˽ͧѲ�������캣�߽���l��һ���ϱ������ֱ�ߣ�3.8�����A�����������䱱ƫ��30�㷽�����4�����B����һ��˽���������ܣ���˽ͧ����������֪��˽ͧ�����������˽������ٵ�3�������輩˽ͧ����˽������ֱ�߷���������ٺ��У� 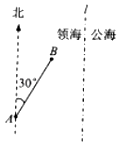
��1������˽���������������룬��ȷ����˽ͧ��������ʹ�������ʱ�����캣�����سɹ������ο����ݣ�sin17��� ![]() ��
�� ![]() ��5.7446��
��5.7446��
��2���ʣ�������˽���غη������ܣ���˽ͧ�Ƿ��������캣�ڳɹ����أ���˵�����ɣ�
���𰸡�
��1���⣺�輩˽ͧ��C������˽����������AC=3BC��
��ABC�У������Ҷ����ɵ�sin��BAC= ![]() =
= ![]() ��
��
���BAC=17�㣬
�༩˽ͧӦ��ƫ��47�㷽������
��ABC�У������Ҷ����ɵ�cos120��= ![]() ����BC��1.68615��
����BC��1.68615��
B���߽���l�ľ���Ϊ3.8��4sin30��=1.8��
��1.68615��1.8��
�������ʱ�����캣�����سɹ�
��2���⣺��AΪԭ�㣬������ͼ��ʾ������ϵ����B��2��2 ![]() �����輩˽ͧ��P��x��y��������˽����������PA=3PB��
�����輩˽ͧ��P��x��y��������˽����������PA=3PB��
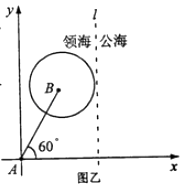
��x2+y2=9[��x��2��2+��y��2 ![]() ��2]������x��
��2]������x�� ![]() ��2+��y��
��2+��y�� ![]() ��2=
��2= ![]() ��
��
��P�Ĺ켣���ԣ� ![]() ��
�� ![]() ��ΪԲ�ģ�
��ΪԲ�ģ� ![]() Ϊ�뾶��Բ��
Ϊ�뾶��Բ��
��Բ�ĵ��߽���l��x=3.8�ľ���Ϊ1.55������Բ�İ뾶��
��������˽���غη������ܣ���˽ͧ�������캣�ڳɹ����أ�
����������1���輩˽ͧ��C������˽����������AC=3BC����ABC�У������Ҷ��������Ҷ���������⣻��2����������ϵ�����P�Ĺ켣���̣����ɽ����

 ������ӱ������ͯ������ϵ�д�
������ӱ������ͯ������ϵ�д� A�ӽ��� ϵ�д�
A�ӽ��� ϵ�д� ȫ�Ų��Ծ�ϵ�д�
ȫ�Ų��Ծ�ϵ�д�����Ŀ��Ϊ���ռ�����֪ʶ����ǿ������ʶ��ijУ�����Ƽװ��ȡ60�ˣ����Ŀ��Ұ��ȡ50�˲μӻ���֪ʶ���ԣ�
��������Ŀ�����������2��2�����������ݴ��ж��Ƿ���99%�İ�����Ϊ����֪ʶ�ɼ�������ѧ�������������йأ�
�������� | ���������� | �ܼ� | |
�װ� | |||
�Ұ� | 30 | ||
�ܼ� | 60 |
��������֪A��B��C���˻������ĸ��ʷֱ�Ϊ ![]() �����������X��ʾA��B��C�����л���������������X�ķֲ��м�����E��X����
�����������X��ʾA��B��C�����л���������������X�ķֲ��м�����E��X����
���� ![]() ��n=a+b+c+d
��n=a+b+c+d
P��K2��k0�� | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |



