题目内容
(本小题满分12分)设函数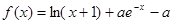 ,
,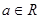 .
.
(Ⅰ)当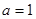 时,证明
时,证明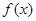 在
在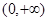 是增函数;
是增函数;
(Ⅱ)若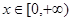 ,
,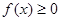 ,求
,求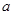 的取值范围.
的取值范围.
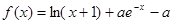 ,
,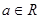 .
.(Ⅰ)当
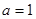 时,证明
时,证明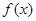 在
在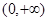 是增函数;
是增函数;(Ⅱ)若
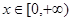 ,
,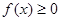 ,求
,求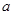 的取值范围.
的取值范围.(Ⅰ)见解析;
(Ⅱ)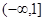
(Ⅱ)
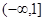
(1)求出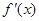 ,然后证明
,然后证明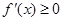 在
在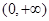 上恒成立即可.
上恒成立即可.
(2)本小题本质是求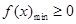 ,
,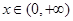 .然后利用导数研究f(x)的极值最值即可.由于含有参数a,需要对a的范围进行讨论.
.然后利用导数研究f(x)的极值最值即可.由于含有参数a,需要对a的范围进行讨论.
(1)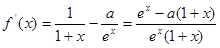 ,
,
当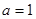 时,
时, 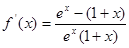 , ---------2分
, ---------2分
令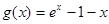 ,则
,则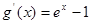 ,
,
当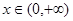 时,
时,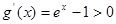 ,所以
,所以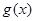 在
在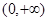 为增函数,
为增函数,
因此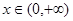 时,
时,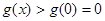 ,所以当
,所以当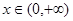 时,
时,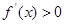 ,
,
则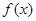 在
在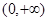 是增函数. ---------6分
是增函数. ---------6分
(2)由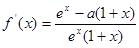 ,
,
由(1)知,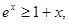 当且仅当
当且仅当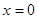 等号成立.
等号成立.
故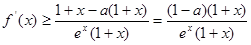 ,
,
从而当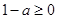 ,即
,即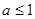 时,
时,
对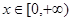 ,
,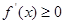 ,
,
于是对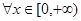
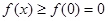 .
.
由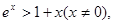 得
得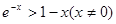 ,
,
从而当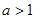 时,
时,
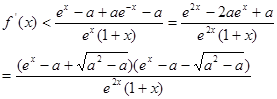
故当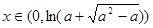 时,
时,
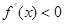 ,
,
于是当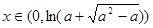 时,
时,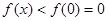 ,
,
综上,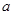 的取值范围是
的取值范围是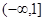 .---------12分
.---------12分
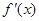 ,然后证明
,然后证明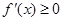 在
在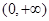 上恒成立即可.
上恒成立即可.(2)本小题本质是求
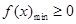 ,
,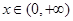 .然后利用导数研究f(x)的极值最值即可.由于含有参数a,需要对a的范围进行讨论.
.然后利用导数研究f(x)的极值最值即可.由于含有参数a,需要对a的范围进行讨论.(1)
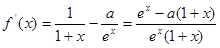 ,
,当
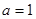 时,
时, 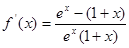 , ---------2分
, ---------2分令
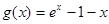 ,则
,则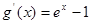 ,
,当
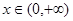 时,
时,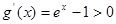 ,所以
,所以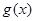 在
在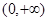 为增函数,
为增函数,因此
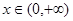 时,
时,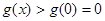 ,所以当
,所以当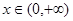 时,
时,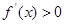 ,
,则
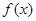 在
在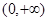 是增函数. ---------6分
是增函数. ---------6分(2)由
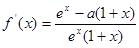 ,
,由(1)知,
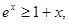 当且仅当
当且仅当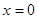 等号成立.
等号成立.故
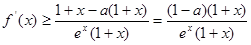 ,
,从而当
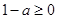 ,即
,即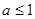 时,
时,对
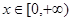 ,
,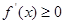 ,
,于是对
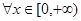
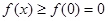 .
.由
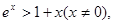 得
得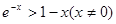 ,
,从而当
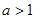 时,
时,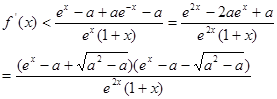
故当
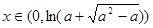 时,
时,
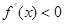 ,
,于是当
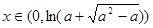 时,
时,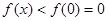 ,
,综上,
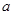 的取值范围是
的取值范围是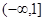 .---------12分
.---------12分
练习册系列答案
相关题目
 ,
, ,其中|t|≤1,将f(x)的最小值记为g(t).
,其中|t|≤1,将f(x)的最小值记为g(t).  成立?如果存在,求出这样的a及其对应的t;如果不存在,请说明理由.
成立?如果存在,求出这样的a及其对应的t;如果不存在,请说明理由. 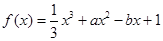 (
(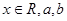 为实数)有极值,且在
为实数)有极值,且在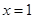 处的切线与直线
处的切线与直线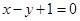 平行.
平行.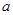 的取值范围;
的取值范围;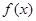 的极小值为
的极小值为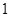 ,若存在,求出实数
,若存在,求出实数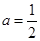 ,
,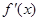 ,令
,令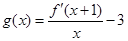
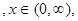
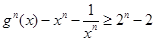
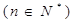
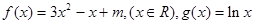
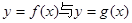 有公共切线时,求函数
有公共切线时,求函数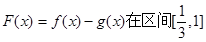 上的最值
上的最值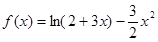 .
.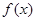 在[0,1]上的极值;
在[0,1]上的极值;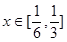 ,不等式
,不等式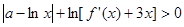 成立,求实数
成立,求实数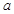 的取值范围;
的取值范围;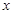 的方程
的方程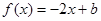 在[0,1]上恰有两个不同的实根,求实数
在[0,1]上恰有两个不同的实根,求实数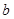 的取值范围.
的取值范围.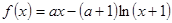 ,其中
,其中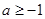 ,求
,求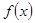 的单调区间。
的单调区间。 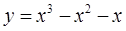 的单调递增区间为_______________
的单调递增区间为_______________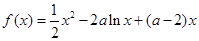 ,
,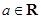 .
.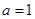 时,求函数
时,求函数 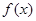 的最小值;
的最小值; 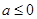 时,讨论函数
时,讨论函数 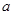 ,对任意的
,对任意的 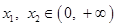 ,且
,且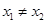 ,有
,有 ,恒成立,若存在求出
,恒成立,若存在求出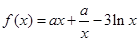 .
.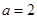 时,求函数
时,求函数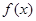 的最小值;
的最小值;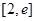 上单调递增,求实数
上单调递增,求实数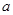 的取值范围.
的取值范围.