题目内容
(本小题满分14分)
在一个半径为1的半球材料中截取三个高度均为h的圆柱,其轴截面如图所示,设三个圆柱体积之和为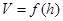 。
。
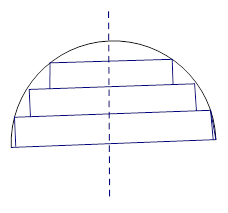
(1) 求f(h)的表达式,并写出h的取值范围是 ;
(2) 求三个圆柱体积之和V的最大值;
在一个半径为1的半球材料中截取三个高度均为h的圆柱,其轴截面如图所示,设三个圆柱体积之和为
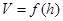 。
。
(1) 求f(h)的表达式,并写出h的取值范围是 ;
(2) 求三个圆柱体积之和V的最大值;
(1) 的取值范围是
的取值范围是 ;⑵三个圆柱体积和
;⑵三个圆柱体积和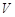 的最大值为
的最大值为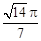 .
.
 的取值范围是
的取值范围是 ;⑵三个圆柱体积和
;⑵三个圆柱体积和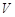 的最大值为
的最大值为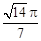 .
.本试题是以半球为背景,表示圆柱体的高度的关系式,以及体积的运用,并结合导数来求解最值问题。
(1)利用球的半径和圆柱的高度得到关于r与半径的关系式,从而得到高度的表示。
(2)而圆柱体的体积就是底面积乘以高,那么三个柱体的体积可以借助于第一问中的高度表示出来,再集合导数的思想求解体积的最值。
解:(1)自下而上三个圆柱的底面半径分别为:
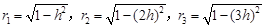 . ………………………………3分
. ………………………………3分
它们的高均为 ,所以体积和
,所以体积和

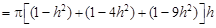
 6分
6分
因为 ,所以
,所以 的取值范围是
的取值范围是 ; ………………………………………7分
; ………………………………………7分
⑵ 由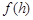
 得
得
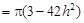
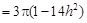 , ………………9分
, ………………9分
又 ,所以
,所以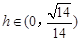 时,
时, ;
; 时,
时, .11分
.11分
所以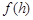 在
在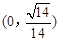 上为增函数,在
上为增函数,在 上为减函数,
上为减函数,
所以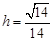 时,
时,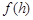 取最大值,
取最大值,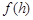 的最大值为
的最大值为 . ………13分
. ………13分
答:三个圆柱体积和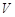 的最大值为
的最大值为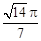 . …………………………………………14分
. …………………………………………14分
(1)利用球的半径和圆柱的高度得到关于r与半径的关系式,从而得到高度的表示。
(2)而圆柱体的体积就是底面积乘以高,那么三个柱体的体积可以借助于第一问中的高度表示出来,再集合导数的思想求解体积的最值。
解:(1)自下而上三个圆柱的底面半径分别为:
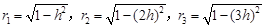 . ………………………………3分
. ………………………………3分它们的高均为
 ,所以体积和
,所以体积和
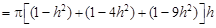
 6分
6分因为
 ,所以
,所以 的取值范围是
的取值范围是 ; ………………………………………7分
; ………………………………………7分⑵ 由
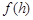
 得
得
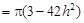
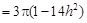 , ………………9分
, ………………9分又
 ,所以
,所以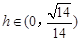 时,
时, ;
; 时,
时, .11分
.11分所以
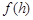 在
在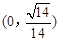 上为增函数,在
上为增函数,在 上为减函数,
上为减函数,所以
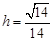 时,
时,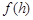 取最大值,
取最大值,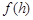 的最大值为
的最大值为 . ………13分
. ………13分答:三个圆柱体积和
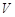 的最大值为
的最大值为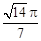 . …………………………………………14分
. …………………………………………14分
练习册系列答案
相关题目
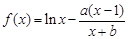 .
.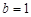 时,若函数
时,若函数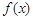 在
在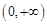 上为单调增函数,求
上为单调增函数,求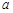 的取值范围;
的取值范围;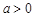 且
且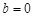 时,求证:函数f (x)存在唯一零点的充要条件是
时,求证:函数f (x)存在唯一零点的充要条件是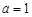 ;
;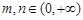 ,且
,且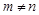 ,求证:
,求证: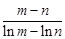 <
<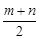 .
.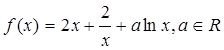 。
。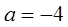 ,求函数
,求函数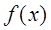 的单调区间;
的单调区间;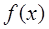 在
在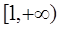 上单调递增,求实数
上单调递增,求实数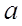 的取值范围;
的取值范围;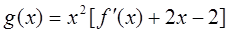 ,若
,若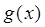 的最小值是
的最小值是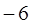 ,求函数
,求函数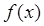 的解析式。
的解析式。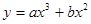 ,当
,当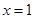 时,有极大值
时,有极大值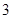 ;
;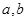 的值;(2)求函数
的值;(2)求函数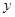 的极小值。
的极小值。 是定义在
是定义在 上的可导函数,且满足
上的可导函数,且满足 . 若
. 若 且
且 ,则
,则



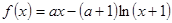 ,其中
,其中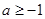 ,求
,求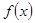 的单调区间。
的单调区间。 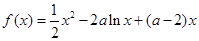 ,
,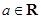 .
.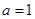 时,求函数
时,求函数 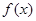 的最小值;
的最小值; 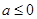 时,讨论函数
时,讨论函数 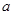 ,对任意的
,对任意的 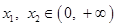 ,且
,且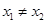 ,有
,有 ,恒成立,若存在求出
,恒成立,若存在求出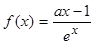 .
.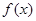 的单调区间;
的单调区间;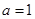 时,若方程
时,若方程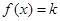 有两个不同的实根
有两个不同的实根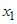 和
和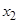 ,
,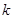 的取值范围;
的取值范围;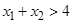 .
.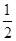 x2
x2 ㏑x的单调递减区间为
㏑x的单调递减区间为 1,1]
1,1]