题目内容
4.曲线$\left\{\begin{array}{l}{x=5cosθ}\\{y=4sinθ}\end{array}\right.$(θ为参数)的离心率是( )| A. | $\frac{4}{5}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{4}$ |
分析 将椭圆的参数方程$\left\{\begin{array}{l}{x=5cosθ}\\{y=4sinθ}\end{array}\right.$(θ为参数)化为标准方程即可求得其离心率.
解答 解:由$\left\{\begin{array}{l}{x=5cosθ}\\{y=4sinθ}\end{array}\right.$(θ为参数),得
$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1,
∴a=5,b=4,c=$\sqrt{25-16}$=3,
∴它的离心率e=$\frac{c}{a}$=$\frac{3}{5}$.
故选:C.
点评 本题考查椭圆的参数方程,考查椭圆的离心率,转化为标准方程是关键,属于中档题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
9.经过如图程序,变量y的值为( )
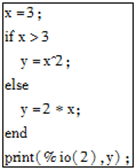
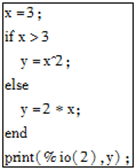
| A. | 3 | B. | 6 | C. | 9 | D. | 27 |
16.已知Sn是等差数列{an}的前n项和,若a2015=S2015=2015,则首项a1=( )
| A. | 2015 | B. | -2015 | C. | 2013 | D. | -2013 |
14.已知函数f(x)=log2(3x+$\frac{1}{{3}^{x}}$-m)的值域为R,则m的取值范围是( )
| A. | (-∞,-2) | B. | (-2,2) | C. | [2,+∞) | D. | (-∞,+∞) |
 如图,是某市1000户居民月平均用电量的频率分布直方图,
如图,是某市1000户居民月平均用电量的频率分布直方图,