题目内容
1.已知{$\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}$}为单位正交基底,$\overrightarrow{a}$=3$\overrightarrow{i}$+2$\overrightarrow{j}$-$\overrightarrow{k}$,$\overrightarrow{b}$=$\overrightarrow{i}$-$\overrightarrow{j}$+2$\overrightarrow{k}$,则5$\overrightarrow{a}$与3$\overrightarrow{b}$的数量积等于( )| A. | -5 | B. | -15 | C. | -3 | D. | -1 |
分析 由已知{$\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}$}为单位正交基底,得到三个向量的坐标,将5$\overrightarrow{a}$与3$\overrightarrow{b}$用坐标表示后,利用数量积公式解答.
解答 解:因为已知{$\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}$}为单位正交基底,设$\overrightarrow{i}$=(1,0,0),$\overrightarrow{j}$(0,1,0),$\overrightarrow{k}$(0,0,1),
所以$\overrightarrow{a}$=3$\overrightarrow{i}$+2$\overrightarrow{j}$-$\overrightarrow{k}$=(3,2,-1),$\overrightarrow{b}$=$\overrightarrow{i}$-$\overrightarrow{j}$+2$\overrightarrow{k}$=(1,-1,2),
所以5$\overrightarrow{a}$=(15,10,-5),3$\overrightarrow{b}$=(3,-3,6),
所以5$\overrightarrow{a}$与3$\overrightarrow{b}$的数量积为:15×3-10×3-5×6=-15;
故选:B.
点评 本题考查了空间向量的数量积;关键是由已知{$\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}$}为单位正交基底,得到它们各自的坐标,将所求用坐标表示.

| A. | 26 | B. | 25 | C. | 24 | D. | 23 |
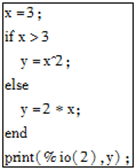
| A. | 3 | B. | 6 | C. | 9 | D. | 27 |
| A. | 2015 | B. | -2015 | C. | 2013 | D. | -2013 |
| A. | -2f′(2) | B. | 2f′(2) | C. | -$\frac{1}{2}$f′(2) | D. | $\frac{1}{2}$f′(2) |