题目内容

18．已知y=f（x）是R上的奇函数，又是周期为2的周期函数，当x∈[0，1]时，f（x）=2x-1，求f（1.5）的值．

分析 根据函数奇偶性和周期性之间的关系进行转化求解即可．

解答 解：∵f（x）是R上的奇函数，又是周期为2的周期函数，
∴f（1.5）=f（1.5-2）=f（-0.5）=-f（0.5）=-（20.5-1）=1-$\sqrt{2}$．

点评 本题主要考查函数值的计算，根据函数的奇偶性和周期性进行转化是解决本题的关键．

练习册系列答案
相关题目
7．已知a为实数，函数f（x）=（x2+1）（x+a）．若f′（-1）=0，求函数y=f（x）在[-$\frac{3}{2}$，1]上的最大值．
9．经过如图程序，变量y的值为（　　）
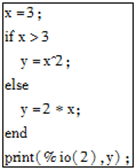
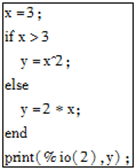
A．3B．6C．9D．27
6．设函数f（x）在x处导数存在，则$\underset{lim}{△x→0}$$\frac{f（2）-f（2+△x）}{2△x}$=（　　）
A．-2f′（2）B．2f′（2）C．-$\frac{1}{2}$f′（2）D．$\frac{1}{2}$f′（2）
13．已知函数f（x）=x2-2|x|．
（1）判断并证明函数的奇偶性；
（2）画出函数图象；
（3）求函数f（x）的值域和单调区间．
3．函数f（x）=x2+ax+b，（x∈R），有两个不等的实数根，都在（0，1）之间．求b2+ab+b的取值范围．
10．计算：cos$\frac{25π}{6}$+cos$\frac{25π}{3}$+tan（-$\frac{25π}{4}$）+sin（-$\frac{7π}{3}$）cos（-$\frac{13π}{6}$）-sin（-$\frac{5π}{6}$）cos（-$\frac{5π}{3}$）．
7．已知直线l1：2x+a2y+1=0，l2：ax-y-3=0，a=2是直线l1与直线l2垂直的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．非充分非必要条件
8．某时段内共有100辆汽车经过某一雷达测速区域，将测得的汽车时速绘制成如图所示的频率分布直方图．根据图形推断，该时段时速不超过50km/h的汽车辆数为23．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网