Question

【题目】已知函数f（x）=loga（x+1），g（x）=loga（1﹣x）其中（a＞0且a≠1）．
（1）求函数f（x）+g（x）的定义域；
（2）判断f（x）+g（x）的奇偶性，并说明理由；
（3）求使f（x）﹣g（x）＞0成立的x的集合．

Answer 1

【答案】
（1）解：f（x）+g（x）=loga（x+1）+loga（1﹣x）．

若要上式有意义，则 ，

即﹣1＜x＜1．

所以所求定义域为{x|﹣1＜x＜1}

（2）解：设F（x）=f（x）+g（x），

则F（﹣x）=f（﹣x）+g（﹣x）

=loga（﹣x+1）+loga（1+x）=F（x）．

所以f（x）+g（x）是偶函数

（3）解：f（x）﹣g（x）＞0，

即loga（x+1）﹣loga（1﹣x）＞0，

loga（x+1）＞loga（1﹣x）．

当0＜a＜1时，上述不等式等价于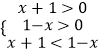

解得﹣1＜x＜0．

当a＞1时，原不等式等价于 ，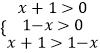

解得0＜x＜1．

综上所述，当0＜a＜1时，原不等式的解集为{x|﹣1＜x＜0}；

当a＞1时，原不等式的解集为{x|0＜x＜1}

【解析】（1）要求函数f（x）+g（x）的定义域，我们可根据让函数解析式有意义的原则，构造不等式组，解不等式组即可得到函数f（x）+g（x）的定义域；（2）要判断f（x）+g（x）的奇偶性，我们根据奇偶性的定义，先判断其定义域是否关于原点对称，然后再判断f（﹣x）+g（﹣x）与f（x）+g（x）的关系，结合奇偶性的定义进行判断；（3）若f（x）﹣g（x）＞0，则我们可以得到一个对数不等式，然后分类讨论底数取值，即可得到不等式的解．