题目内容
【题目】已知0<a<1,函数f(x)=loga(ax﹣1)
(I)求函数f(x)的定义域;
(Ⅱ)判断f(x)的单调性;
(Ⅲ)若m满足f(1﹣m)≥f(1﹣m2),求m的范围.
【答案】解:(Ⅰ)由ax﹣1>0,得ax>1,
因为0<a<1,所以x<0,
所以f(x)定义域为(﹣∞,0)
(Ⅱ)设y=logaU,U=ax﹣1
因为0<a<1,y=logaU是减函数,U=ax﹣1是减函数,
所以 ![]() 是(﹣∞,0)上的增函数
是(﹣∞,0)上的增函数
(Ⅲ)由(2)知f(x)是(﹣∞,0)上的增函数,
所以 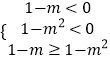 ,解得:m>1
,解得:m>1
【解析】(Ⅰ)根据对数函数的性质求出函数的定义域即可;(Ⅱ)根据复合函数同增异减的原则,结合换元法判断出f(x)的单调性即可;(Ⅲ)根据函数的单调性以及对数函数的性质得到关于m的不等式组,解出即可.
【考点精析】掌握对数函数的定义域和对数函数的单调区间是解答本题的根本,需要知道对数函数的定义域范围:(0,+∞);a变化对图象的影响:在第一象限内,a越大图象越靠低;在第四象限内,a越大图象越靠高.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目