题目内容
设A、B分别为椭圆
＝1(a>b>0)的左、右顶点，椭圆长半轴的长等于焦距，且直线x＝4是它的右准线．
(1)求椭圆的方程；
(2)设P为椭圆右准线上不同于点(4，0)的任意一点，若直线BP与椭圆相交于两点B、N，求证：∠NAP为锐角．
＝1(a>b>0)的左、右顶点，椭圆长半轴的长等于焦距，且直线x＝4是它的右准线．(1)求椭圆的方程；
(2)设P为椭圆右准线上不同于点(4，0)的任意一点，若直线BP与椭圆相交于两点B、N，求证：∠NAP为锐角．
（1）
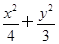＝1（2）见解析
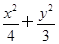＝1（2）见解析(1)解：依题意，得
解得
从而b＝
，故椭圆的方程为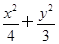＝1.
(2)证明：由(1)得A(－2，0)，B(2，0)，设N(x0，y0)，
∵N点在椭圆上，∴
＝
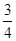(4－
)．又N点异于顶点A、B，
∴－2<x0<2，y0≠0.由P、B、N三点共线可得P
，从而
＝(x0＋2，y0)，
＝
，则·＝6x0＋12＋
＝6x0＋12－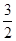
(2＋x0)＝
(x0＋2)．
∵x0＋2>0，y0≠0，∴·>0，于是∠NAP为锐角．
解得从而b＝，故椭圆的方程为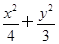＝1.(2)证明：由(1)得A(－2，0)，B(2，0)，设N(x0，y0)，
∵N点在椭圆上，∴
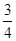＝(4－)．又N点异于顶点A、B，∴－2<x0<2，y0≠0.由P、B、N三点共线可得P
，从而＝(x0＋2，y0)，＝，则·＝6x0＋12＋＝6x0＋12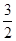－(2＋x0)＝(x0＋2)．∵x0＋2>0，y0≠0，∴
·>0，于是∠NAP为锐角．
练习册系列答案
阅读快车系列答案
相关题目
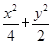＝1的顶点，过坐标原点的直线交椭圆于P、A两点，其中P在第一象限，过P作x轴的垂线，垂足为C，连结AC，并延长交椭圆于点B，设直线PA的斜率为k.
和点
分别为椭圆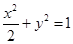
的中心和右焦点，点
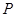为椭圆上的任意一点，则
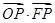的最小值为（ ）
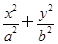＝1(a＞b＞c＞0，a2＝b2＋c2)的左、右焦点分别为F1，F2，若以F2为圆心，b－c为半径作圆F2，过椭圆上一点P作此圆的切线，切点为T，且PT的最小值为
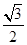(a－c)，则椭圆的离心率e的取值范围是________．
＝1(a>b>0)的左、右焦点，A，B分别是椭圆E的左、右顶点，且
＋5
＝0.
是椭圆
的半焦距，则
的取值范围为 .
，且G上一点到G的两个焦点的距离之和为12，则椭圆G的方程为______________．