题目内容
14.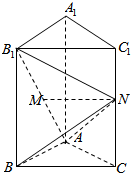 如图,在正三棱柱ABC-A1B1C1中,AA1=2AB,N是CC1的中点,M是线段AB1上的动点(与端点不重合),且AM=λAB1.
如图,在正三棱柱ABC-A1B1C1中,AA1=2AB,N是CC1的中点,M是线段AB1上的动点(与端点不重合),且AM=λAB1.(1)若$λ=\frac{1}{2}$,求证:MN⊥AA1;
(2)若直线MN与平面ABN所成角的大小为θ,求sinθ的最大值.
分析 (1)如图,建立空间直角系,给出相应点的坐标,只要证明$\overrightarrow{MN}•\overrightarrow{A{A_1}}=0$,即可得出MN⊥AA1.
(2)设平面ABN的法向量$\overrightarrow n=(x,y,z)$,利用$\left\{\begin{array}{l}\overrightarrow n•\overrightarrow{AB}=0\\ \overrightarrow n•\overrightarrow{AN}=0\end{array}\right.$,可得$\overrightarrow{n}$.利用$sinθ=|{cos?\overrightarrow{MN},\overrightarrow n>}|$=$\frac{|\overrightarrow{MN}•\overrightarrow{n}|}{|\overrightarrow{MN}||\overrightarrow{n}|}$即可得出.
解答 (1)证明:如图,建立空间直角系,则
${B_1}(1,0,2),M(λ,0,2λ),B(1,0,0),N(\frac{1}{2},\frac{{\sqrt{3}}}{2},1),{A_1}(0,0,2)$.
当$λ=\frac{1}{2}$时,$M(\frac{1}{2},0,1)$,此时$\overrightarrow{MN}=(0,\frac{{\sqrt{3}}}{2},0)$,$\overrightarrow{A{A_1}}=(0,0,2)$,
∵$\overrightarrow{MN}•\overrightarrow{A{A_1}}=0$,∴MN⊥AA1.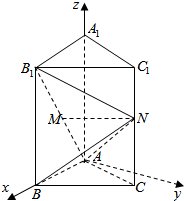
(2)解:设平面ABN的法向量$\overrightarrow n=(x,y,z)$,则$\left\{\begin{array}{l}\overrightarrow n•\overrightarrow{AB}=0\\ \overrightarrow n•\overrightarrow{AN}=0\end{array}\right.$,
即$\left\{\begin{array}{l}x=0\\ \frac{{\sqrt{3}}}{2}y+z=0\end{array}\right.$,取$\overrightarrow n=(0,2,\sqrt{3})$.
而$\overrightarrow{MN}=(\frac{1}{2}-λ,\frac{{\sqrt{3}}}{2},1-2λ)$,
∴$sinθ=|cos<\overrightarrow{MN},\overrightarrow{n}>|$=$\frac{{2\sqrt{3}λ}}{{\sqrt{7}•\sqrt{5{λ^2}-5λ+2}}}$=$\frac{{2\sqrt{3}}}{{\sqrt{7}•\sqrt{5-5({\frac{1}{λ}})+2{{({\frac{1}{λ}})}^2}}}}$,
∵0<λ<1,∴$\frac{1}{λ}>1$,
故$sinθ=\frac{{2\sqrt{3}}}{{\sqrt{7}•\sqrt{5-5({\frac{1}{λ}})+2{{({\frac{1}{λ}})}^2}}}}≤\frac{{4\sqrt{6}}}{{\sqrt{105}}}=\frac{{4\sqrt{630}}}{105}$=$\frac{4\sqrt{70}}{35}$,
当且仅当$\frac{1}{λ}=\frac{5}{4}$,即$λ=\frac{4}{5}$时,等号成立.
∴sinθ的最大值为$\frac{4\sqrt{70}}{35}$.
点评 本题考查了建立空间直角坐标系解决线线垂直、线面垂直、空间角、向量坐标运算及其夹角公式,考查了推理能力与计算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案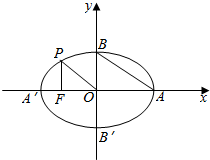 如图,A、A′、B、B′是椭圆的顶点,从椭圆上一点P向x轴作垂线,垂足为焦点F,且AB∥OP,FA′=$\sqrt{10}$-$\sqrt{5}$,求椭圆的标准方程.
如图,A、A′、B、B′是椭圆的顶点,从椭圆上一点P向x轴作垂线,垂足为焦点F,且AB∥OP,FA′=$\sqrt{10}$-$\sqrt{5}$,求椭圆的标准方程.