题目内容
4.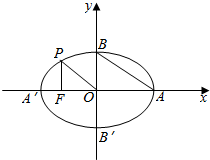 如图,A、A′、B、B′是椭圆的顶点,从椭圆上一点P向x轴作垂线,垂足为焦点F,且AB∥OP,FA′=$\sqrt{10}$-$\sqrt{5}$,求椭圆的标准方程.
如图,A、A′、B、B′是椭圆的顶点,从椭圆上一点P向x轴作垂线,垂足为焦点F,且AB∥OP,FA′=$\sqrt{10}$-$\sqrt{5}$,求椭圆的标准方程.
分析 由题意设出椭圆方程,求出AB,OP所在直线的斜率,由斜率相等得到b=c,再由FA′=$\sqrt{10}$-$\sqrt{5}$得a-c=$\sqrt{10}$-$\sqrt{5}$,然后结合隐含条件求得a,b的值,则椭圆方程可求.
解答 解:由题意可设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$.
∵AB∥OP,∴kAB=kOP,即$-\frac{b}{a}=-\frac{{b}^{2}}{ac}$,也就是b=c ①.
又FA′=$\sqrt{10}$-$\sqrt{5}$,即a-c=$\sqrt{10}$-$\sqrt{5}$ ②.
且a2=b2+c2 ③.
联立①②③可得:$a=\sqrt{10},b=\sqrt{5}$.
∴椭圆的标准方程为$\frac{{x}^{2}}{10}+\frac{{y}^{2}}{5}=1$.
点评 本题考查椭圆标准方程的求法,涉及椭圆方程的求解问题,要注意隐含条件a2=b2+c2的应用,是基础题.

练习册系列答案
相关题目
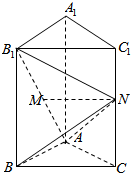 如图,在正三棱柱ABC-A1B1C1中,AA1=2AB,N是CC1的中点,M是线段AB1上的动点(与端点不重合),且AM=λAB1.
如图,在正三棱柱ABC-A1B1C1中,AA1=2AB,N是CC1的中点,M是线段AB1上的动点(与端点不重合),且AM=λAB1.