题目内容
5.已知数列{an}的前n项和为Sn,且Sn=n-5an-85,n∈N*.(1)证明:{an-1}是等比数列;
(2)求数列{an}的通项公式.
分析 (1)通过Sn=n-5an-85与Sn+1=(n+1)-5an+1-85作差、整理得an+1=$\frac{5}{6}$an+$\frac{1}{6}$,变形可知an+1-1=$\frac{5}{6}$(an-1),进而可知数列{an-1}是以-15为首项、$\frac{5}{6}$为公比的等比数列;
(2)通过(1)可知an-1=-15•$(\frac{5}{6})^{n-1}$,进而计算可得结论.
解答 (1)证明:∵Sn=n-5an-85,
∴Sn+1=(n+1)-5an+1-85,
两式相减得:an+1=1+5an-5an+1,
整理得:an+1=$\frac{5}{6}$an+$\frac{1}{6}$,
∴an+1-1=$\frac{5}{6}$(an-1),
又∵a1=1-5a1-85,即a1=-14,
∴a1-1=-14-1=-15,
∴数列{an-1}是以-15为首项、$\frac{5}{6}$为公比的等比数列;
(2)解:由(1)可知an-1=-15•$(\frac{5}{6})^{n-1}$,
∴an=1-15•$(\frac{5}{6})^{n-1}$.
点评 本题考查数列的通项,注意解题方法的积累,属于中档题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
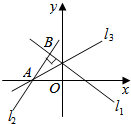 如果直线l1的倾斜角是150°,l2⊥l1,垂足为B,l1,l2与x轴分别相交于点C,A,l3平分∠BAC,则l3的倾斜角为30°.
如果直线l1的倾斜角是150°,l2⊥l1,垂足为B,l1,l2与x轴分别相交于点C,A,l3平分∠BAC,则l3的倾斜角为30°.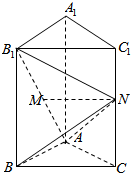 如图,在正三棱柱ABC-A1B1C1中,AA1=2AB,N是CC1的中点,M是线段AB1上的动点(与端点不重合),且AM=λAB1.
如图,在正三棱柱ABC-A1B1C1中,AA1=2AB,N是CC1的中点,M是线段AB1上的动点(与端点不重合),且AM=λAB1.