题目内容
9.在△ABC中,D是BC边上一点,BD=3DC,若P是AD边上一动点,且AD=2,则$\overrightarrow{PA}•(\overrightarrow{PB}+3\overrightarrow{PC})$的最小值为-4.分析 通过向量的数量积以及向量的表示,化简数量积,利用BD=3DC,令$|\overrightarrow{PA}|=t$,转化数量积为t的二次函数,然后求解最小值.
解答 解:由于$\overrightarrow{PA}•(\overrightarrow{PB}+3\overrightarrow{PC})=\overrightarrow{PA}•[\overrightarrow{PB}+3(\overrightarrow{PD}+\overrightarrow{DC})]=\overrightarrow{PA}•[(\overrightarrow{PB}+3\overrightarrow{DC})+3\overrightarrow{PD}]$,
因为BD=3DC,所以$\overrightarrow{PB}+3\overrightarrow{DC}=\overrightarrow{PB}+\overrightarrow{BD}=\overrightarrow{PD}$,
故$\overrightarrow{PA}•(\overrightarrow{PB}+3\overrightarrow{PC})=4\overrightarrow{PA}•\overrightarrow{PD}$,
令$|\overrightarrow{PA}|=t$,
则$\overrightarrow{PA}•(\overrightarrow{PB}+3\overrightarrow{PC})$=4•t•(2-t)•cos180°=4[(t-1)2-1]≥-4.
故答案为:-4.
点评 本题考查平面向量的数量积的应用,二次函数的最值的求法,考查转化思想以及计算能力.

练习册系列答案
相关题目
1.在某次测验中,有6为同学的平均成绩为75分.用xn表示编号为n(n=1,2,…,6)的同学所得成绩,且前5位同学的成绩如下:求第6位同学成绩x6是( )
| 编号n | 1 | 2 | 3 | 4 | 5 |
| 成绩xn | 74 | 76 | 72 | 70 | 78 |
| A. | 80 | B. | 90 | C. | 86 | D. | 70 |
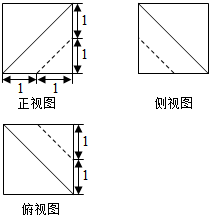
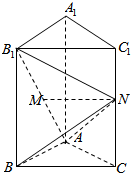 如图,在正三棱柱ABC-A1B1C1中,AA1=2AB,N是CC1的中点,M是线段AB1上的动点(与端点不重合),且AM=λAB1.
如图,在正三棱柱ABC-A1B1C1中,AA1=2AB,N是CC1的中点,M是线段AB1上的动点(与端点不重合),且AM=λAB1.