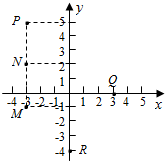题目内容
6.已知a是实数,如果任意实数x都是不等式|x+1|+|x|-|x+a|>0的解,求实数a的取值范围.分析 令f(x)=|x+1|+|x|=$\left\{\begin{array}{l}{-2x-1,x<-1}\\{1,-1≤x<0}\\{2x+1,x≥0}\end{array}\right.$,g(x)=|x+a|,则由题意可得函数f(x)的图象横在函数g(x)的图象的上方,数形结合求得a的范围.
解答  解:由题意可得不等式|x+1|+|x|>|x+a|恒成立.
解:由题意可得不等式|x+1|+|x|>|x+a|恒成立.
令f(x)=|x+1|+|x|=$\left\{\begin{array}{l}{-2x-1,x<-1}\\{1,-1≤x<0}\\{2x+1,x≥0}\end{array}\right.$,g(x)=|x+a|,
则函数f(x)的图象横在函数g(x)的图象的上方,
A (0,1)、B(-1,1),
如图所示:
由题意可得-1<-a<0,
求得0<a<1.
点评 本题主要考查带有绝对值的函数,函数的恒成立问题,体现了转化、数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
1.在某次测验中,有6为同学的平均成绩为75分.用xn表示编号为n(n=1,2,…,6)的同学所得成绩,且前5位同学的成绩如下:求第6位同学成绩x6是( )
| 编号n | 1 | 2 | 3 | 4 | 5 |
| 成绩xn | 74 | 76 | 72 | 70 | 78 |
| A. | 80 | B. | 90 | C. | 86 | D. | 70 |
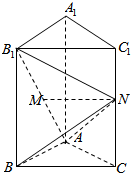 如图,在正三棱柱ABC-A1B1C1中,AA1=2AB,N是CC1的中点,M是线段AB1上的动点(与端点不重合),且AM=λAB1.
如图,在正三棱柱ABC-A1B1C1中,AA1=2AB,N是CC1的中点,M是线段AB1上的动点(与端点不重合),且AM=λAB1.