题目内容
3.在数列{an}中,a1=-2,an+1=$\frac{1+{a}_{n}}{1-{a}_{n}}$,则a2016=3.分析 通过计算出前几项的值确定周期,进而计算可得结论.
解答 解:依题意,a2=$\frac{1+{a}_{1}}{1-{a}_{1}}$=$\frac{1-2}{1+2}$=-$\frac{1}{3}$,
a3=$\frac{1+{a}_{2}}{1-{a}_{2}}$=$\frac{1-\frac{1}{3}}{1+\frac{1}{3}}$=$\frac{1}{2}$,
a4=$\frac{1+{a}_{3}}{1-{a}_{3}}$=$\frac{1+\frac{1}{2}}{1-\frac{1}{2}}$=3,
a5=$\frac{1+{a}_{4}}{1-{a}_{4}}$=$\frac{1+3}{1-3}$=-2,
∴数列{an}是以4为周期的周期数列,
又∵2016=504×4,
∴a2016=a4=3,
故答案为:3.
点评 本题考查数列的通项,注意解题方法的积累,属于中档题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
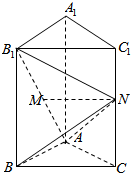 如图,在正三棱柱ABC-A1B1C1中,AA1=2AB,N是CC1的中点,M是线段AB1上的动点(与端点不重合),且AM=λAB1.
如图,在正三棱柱ABC-A1B1C1中,AA1=2AB,N是CC1的中点,M是线段AB1上的动点(与端点不重合),且AM=λAB1.