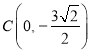题目内容
【题目】已知函数f(x)=aex﹣x,
(1)求f(x)的单调区间,
(2)若关于x不等式aex≥x+b对任意![]() 和正数b恒成立,求
和正数b恒成立,求![]() 的最小值.
的最小值.
【答案】(1)答案见解析.(2)![]()
【解析】
(1)先求导,再分类讨论,根据导数和函数单调性的关系即可求出;
(2)先根据(1)利用导数和函数最值的关系求出![]() ,可得
,可得![]() ,设
,设![]() ,利用导数求出函数的最小值即可.
,利用导数求出函数的最小值即可.
(1)f′(x)=aex﹣1,
当a≤0时,![]() <0,f(x)在R上单调递减,
<0,f(x)在R上单调递减,
若a>0时,令![]() =aex﹣1=0,x=﹣lna,
=aex﹣1=0,x=﹣lna,
在x>﹣lna时,![]() >0,f(x)为增函数,
>0,f(x)为增函数,
在x<﹣lna时,![]() <0,f(x)为减函数,
<0,f(x)为减函数,
所以,当![]() 时,
时,![]() 的单调减区间为
的单调减区间为![]() ,无增区间;
,无增区间;
当![]() 时,
时,![]() 的单调减区间为
的单调减区间为![]() ,增区间为
,增区间为![]() .
.
(2)f(x)=aex﹣x,由题意f(x)min≥b,
由(1)可知,当a≤0时,f(x)在R上单调递减,无最小值,不符合题意,
当a>0时,f(x)min=f(﹣lna)=1+lna≥b,
∴![]() ,
,
设h(a)![]() ,则
,则![]()
![]() ,
,
a∈(0,1],![]() <0;a∈[1,+∞),
<0;a∈[1,+∞),![]() ≥0,
≥0,
∴h(a)min=h(1)=1.
所以![]() 的最小值为
的最小值为![]() .
.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
【题目】假设关于某设备的使用年限x和所支出的维修费用 y(万元),有如下的统计资料:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料可知y对x呈线性相关关系,且线性回归方程为y=a+bx,其中已知b=1.23,请估计使用年限为20年时,维修费用约为_________