题目内容
【题目】某种产品的广告费支出x与销售额y(单位:万元)之间有如表对应数据:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
(1)求广告费支出x与销售额y回归直线方程 ![]() =bx+a(a,b∈R);
=bx+a(a,b∈R);
已知b= 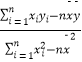 ,
, ![]()
(2)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对值不超过5的概率.
【答案】
(1)解:由题意得 ![]() ,
, ![]() ,
,  ,
,
![]() ,
,
所求回归直线方程为 ![]()
(2)解:基本事件:(30,40),(30,60),(30,50),(30,70),
(40,60),(40,50),(40,70),(60,50),(60,70),(50,70)共10个
两组数据其预测值与实际值之差的绝对值都超过5:(60,50)
所以至少有一组数据其预测值与实际值之差的绝对值不超过5的概率为 ![]()
【解析】(1)首先求出x,y的平均数,利用最小二乘法做出线性回归方程的系数,根据样本中心点满足线性回归方程,代入已知数据求出a的值,写出线性回归方程.(2)分别求出在已有的五组数据中任意抽取两组的情况总数,及至少有一组数据其预测值与实际值之差的绝对值不超过5的情况数,代入古典概型概率计算公式,可得答案.

练习册系列答案
相关题目
【题目】已知X和Y是两个分类变量,由公式K2= ![]() 算出K2的观测值k约为7.822根据下面的临界值表可推断( )
算出K2的观测值k约为7.822根据下面的临界值表可推断( )
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
A.推断“分类变量X和Y没有关系”犯错误的概率上界为0.010
B.推断“分类变量X和Y有关系”犯错误的概率上界为0.010
C.有至少99%的把握认为分类变量X和Y没有关系
D.有至多99%的把握认为分类变量X和Y有关系