��Ŀ����
����Ŀ���������κ���f��x��=ax3+bx2+cx+d��a��0�����������壺��f�䣨x���Ǻ���y=f��x���ĵ�����f��䣨x����f�䣨x���ĵ�����������f��䣨x����ʵ����x0 �� ��Ƶ㣨x0 �� f��x0����Ϊ����y=f��x���ġ��յ㡱��ijͬѧ����̽�����֣��κ�һ�����κ������С��յ㡱���κ�һ�����κ������жԳ����ģ��ҡ��յ㡱���ǶԳ����ģ��躯��f��x��= ![]() x3��
x3�� ![]() x2+3x��
x2+3x�� ![]() �����������һ���֣�����f��
�����������һ���֣�����f�� ![]() ��+f��
��+f�� ![]() ��+f��
��+f�� ![]() ��+��+f��
��+��+f�� ![]() ��= ��
��= ��
���𰸡�2014
���������⣺f�䣨x��=x2��x+3��
��f��䣨x��=2x��1=0��x0= ![]() ��
��
f��x0��=1��
�� ![]() ��1��Ϊf��x���ĶԳ����ģ�����
��1��Ϊf��x���ĶԳ����ģ����� ![]() ��
��
��f�� ![]() ��+f��
��+f�� ![]() ��=2f��
��=2f�� ![]() ��=2��
��=2��
��f�� ![]() ��+f��
��+f�� ![]() ��+f��
��+f�� ![]() ��+��+f��
��+��+f�� ![]() ��=2014��
��=2014��
�ʴ�Ϊ��2014��
��������Ƴ��� ![]() ��1��Ϊf��x���ĶԳ����ģ��Ӷ��ɵ�f��
��1��Ϊf��x���ĶԳ����ģ��Ӷ��ɵ�f�� ![]() ��+f��
��+f�� ![]() ��=2f��
��=2f�� ![]() ��=2���Ӷ���f��
��=2���Ӷ���f�� ![]() ��+f��
��+f�� ![]() ��+f��
��+f�� ![]() ��+��+f��
��+��+f�� ![]() ��=2014��ֵ��
��=2014��ֵ��

 �ŵ������ϵ�д�
�ŵ������ϵ�д� 53������ϵ�д�
53������ϵ�д�����Ŀ��ij�ֲ�Ʒ�Ĺ���֧��x�����۶�y����λ����Ԫ��֮���������Ӧ���ݣ�
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
��1�������֧��x�����۶�y�ع�ֱ�߷��� ![]() =bx+a��a��b��R����
=bx+a��a��b��R����
��֪b= 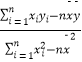 ��
�� ![]()
��2�������е����������������ȡ���飬��������һ��������Ԥ��ֵ��ʵ��ֵ֮��ľ���ֵ������5�ĸ��ʣ�
