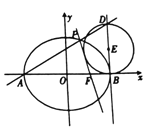
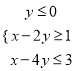题目内容
【题目】设f（x）=|lnx|，若函数g（x）=f（x）﹣ax在区间（0，3]上有三个零点，则实数a的取值范围是（ ）
A.（0， 
）
B.（ 
，e）
C.（0， ]
D.[ ， ）
【答案】D
【解析】解：函数f（x）=|lnx|的图象如图示：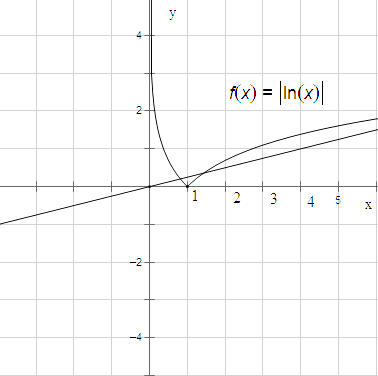 
当a≤0时，显然，不合乎题意，
当a＞0时，如图示，
当x∈（0，1]时，存在一个零点，
当x＞1时，f（x）=lnx，
可得g（x）=lnx﹣ax，（x∈（1，3]）
g′（x）= 
= 
，
若g′（x）＜0，可得x＞ 
，g（x）为减函数，
若g′（x）＞0，可得x＜ ，g（x）为增函数，
此时f（x）必须在[1，3]上有两个零点，
∴ 
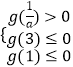
解得， 
，
在区间（0，3]上有三个零点时， ，
故选D．
练习册系列答案
相关题目
【题目】某种产品的广告费支出x与销售额y（单位：万元）之间有如表对应数据：
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
（1）求广告费支出x与销售额y回归直线方程 
=bx+a（a，b∈R）；
已知b=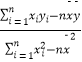 
， 
（2）在已有的五组数据中任意抽取两组，求至少有一组数据其预测值与实际值之差的绝对值不超过5的概率．
