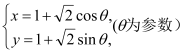Question

【题目】如图（1）,在直角梯形ABCP中,AP∥BC,AP⊥AB,AB=BC=AP=2,D是AP的中点,E,F,G分别是PC,PD,CB的中点,将△PCD沿CD折起,使点P在平面ABCD内的射影为点D,如图（2）．

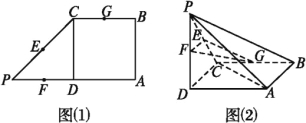
（1）求证:AP∥平面EFG;

（2）求三棱锥P-ABC的体积．

Answer 1

【答案】（1）详见解析（2）

【解析】

试题分析：（I）利用三角形的中位线定理、平行线的传递性、平行四边形的判定定理、线面平行的判定定理等即可得出；（II）由已知点P在平面ABCD上的射影为点D，可得PD⊥平面ABCD．即PD是三棱锥P-ABC的高．利用三棱锥P-ABC的体积V=S△ABC×PD即可得出

试题解析：（I）证明：取AD的中点H，连接FH、GH．

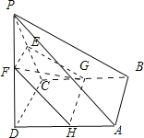
∵E，F，G分别为PC、PD、CB的中点，∴EF∥CD，CGDH，

∴四边形CDHG是平行四边形，∴CD∥GH．

∴EF∥GH．∴四点EFHG四点共面．又FH∥PA．

PA平面EFGH，FH平面EFGH．∴PA∥平面EFGH．

（II）解：∵点P在平面ABCD上的射影为点D，∴PD⊥平面ABCD．

即PD是三棱锥P-ABC的高．

而．

∴三棱锥P-ABC的体积V=．