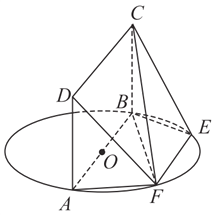
题目内容
【题目】已知椭圆的焦点在x轴上,一个顶点为![]() ,离心率为
,离心率为![]() ,过椭圆的右焦点F的直线l与坐标轴不垂直,且交椭圆于A,B两点.
,过椭圆的右焦点F的直线l与坐标轴不垂直,且交椭圆于A,B两点.
![]() 求椭圆的方程;
求椭圆的方程;
![]() 设点C是点A关于x轴的对称点,在x轴上是否存在一个定点N,使得C,B,N三点共线?若存在,求出定点的坐标;若不存在,说明理由;
设点C是点A关于x轴的对称点,在x轴上是否存在一个定点N,使得C,B,N三点共线?若存在,求出定点的坐标;若不存在,说明理由;
![]() 设
设![]() ,是线段
,是线段![]() 为坐标原点
为坐标原点![]() 上的一个动点,且
上的一个动点,且![]() ,求m的取值范围.
,求m的取值范围.
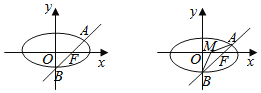
【答案】(1)![]() ;(2)定点
;(2)定点![]() (3)
(3)![]()
【解析】
(1)根据椭圆的一个顶点,即b=1,利用离心率求得a和c关系进而求得a,则椭圆的方程可得;(2)设存在N(t,0),使得C、B、N三点共线,则![]() ∥
∥![]() ,利用向量共线定理可得t
,利用向量共线定理可得t![]() ,即可得出.(3)设直线l的方程为y=k(x﹣2)(k≠0),代入椭圆方程,利用韦达定理结合向量的数量积公式,即可求得m的取值范围;
,即可得出.(3)设直线l的方程为y=k(x﹣2)(k≠0),代入椭圆方程,利用韦达定理结合向量的数量积公式,即可求得m的取值范围;
![]() 由椭圆的焦点在x轴上,设椭圆C的方程为
由椭圆的焦点在x轴上,设椭圆C的方程为![]() ,
,
椭圆C的一个顶点为![]() ,即
,即![]()
由![]() ,解得:
,解得:![]() ,
,
所以椭圆C的标准方程为![]() ;
;
![]() 由得
由得![]() ,设
,设![]() ,
,![]() ,
,
设直线l的方程为![]() ,代入椭圆方程,消去y可得
,代入椭圆方程,消去y可得![]()
则![]() ,
,![]() ,
,
![]() 点C与点A关于x轴对称,
点C与点A关于x轴对称,![]()
假设存在![]() ,使得C、B、N三点共线,
,使得C、B、N三点共线,
则![]() ,
,![]() ,
,
![]() 、B、N三点共线,
、B、N三点共线,
![]() ,
,
![]() ,
,
即![]() ,
,
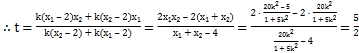 .
.
![]() 存在定点
存在定点![]() ,使得C、B、N三点共线.
,使得C、B、N三点共线.
![]() 由
由![]() ,
,
![]() ,
,![]()
![]() ,
,
![]() ,
,![]()
![]()
![]() ,
,
![]() ,
,
解得:![]() ,
,
![]() 当
当![]() 时,符合题意
时,符合题意
故m的范围为![]()

练习册系列答案
相关题目
【题目】已知函数![]() 的定义域
的定义域![]() ,部分对应值如表,
,部分对应值如表,![]() 的导函数
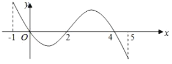
的导函数![]() 的图象如图所示,下列关于函数
的图象如图所示,下列关于函数![]() 的结论正确的是( )
的结论正确的是( )
|
| 0 | 4 | 5 |
| 1 | 2 | 2 | 1 |
A.函数![]() 的极大值点有2个
的极大值点有2个
B.函数![]() 在
在![]() 上是减函数
上是减函数
C.若![]() 时,
时,![]() 的最大值是2,那么
的最大值是2,那么![]() 的最大值为4
的最大值为4
D.当![]() 时,函数
时,函数![]() 有4个零点
有4个零点