题目内容
【题目】在平面直角坐标系![]() 中,
中,![]() ,
,![]() 是曲线段
是曲线段![]() :
:![]() (
(![]() 是参数,
是参数,![]() )的左、右端点,
)的左、右端点,![]() 是
是![]() 上异于
上异于![]() ,
,![]() 的动点,过点
的动点,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() .
.
(1)建立适当的极坐标系,写出点![]() 轨迹的极坐标方程;
轨迹的极坐标方程;
(2)求![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据![]() 的参数方程可得直角坐标方程
的参数方程可得直角坐标方程![]() ,求出端点
,求出端点![]() ,
,![]() ,求在
,求在![]() 处的切线斜率为和与
处的切线斜率为和与![]() 轴的交点坐标,由垂直关系得
轴的交点坐标,由垂直关系得![]() 的轨迹是以线段
的轨迹是以线段![]() 为直径的
为直径的![]() 圆弧(不含端点),由此建立极坐标系,得出极坐标方程.
圆弧(不含端点),由此建立极坐标系,得出极坐标方程.
(2)设直线![]() 与以
与以![]() 为圆心,
为圆心,![]() 为半径的圆交于两点
为半径的圆交于两点![]() ,
,![]() ,则根据半径相等,由相交弦定理,得
,则根据半径相等,由相交弦定理,得![]() ,代入
,代入![]() ,即可得出最大值.
,即可得出最大值.
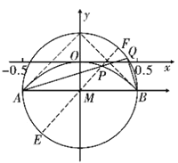
解:(1)如图,曲线段![]() 即为抛物线上一段
即为抛物线上一段![]() ,
,
端点![]() ,
,![]() ,
,
在![]() 处的切线斜率为
处的切线斜率为![]() ,与
,与![]() 轴的交点坐标为
轴的交点坐标为![]() .
.
因为![]() ,所以
,所以![]() 的轨迹是以线段
的轨迹是以线段![]() 为直径的
为直径的![]() 圆弧(不含端点),
圆弧(不含端点),
以线段![]() 的中点
的中点![]() 为极点,射线
为极点,射线![]() 为极轴,建立极坐标系,
为极轴,建立极坐标系,
则![]() 点轨迹的极坐标方程为
点轨迹的极坐标方程为![]() .
.
(2)设直线![]() 与以
与以![]() 为圆心,
为圆心,![]() 为半径的圆交于两点
为半径的圆交于两点![]() ,
,![]() ,
,
则![]() ,
,
由相交弦定理,得![]()
![]()
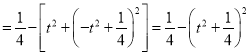 ,
,
当![]() ,即
,即![]() 时,
时,![]() 最大,最大值为
最大,最大值为![]() .
.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
【题目】人们常说的“幸福感指数”就是指某个人主观地评价他对自己目前生活状态的满意程度的指标,常用区间![]() 内的一个数来表示,该数越接近
内的一个数来表示,该数越接近![]() 表示满意度越高.为了解某地区居民的幸福感情况,随机对该地区的男、女居民各
表示满意度越高.为了解某地区居民的幸福感情况,随机对该地区的男、女居民各![]() 人进行了调查,调查数据如表所示:
人进行了调查,调查数据如表所示:
幸福感指数 |
|
|
|
|
|
男居民人数 |
|
|
|
|
|
女居民人数 |
|
|
|
|
|
(1)估算该地区居民幸福感指数的平均值;
(2)若居民幸福感指数不小于![]() ,则认为其幸福.为了进一步了解居民的幸福满意度,调查组又在该地区随机抽取
,则认为其幸福.为了进一步了解居民的幸福满意度,调查组又在该地区随机抽取![]() 对夫妻进行调查,用
对夫妻进行调查,用![]() 表示他们之中幸福夫妻(夫妻二人都感到幸福)的对数,求
表示他们之中幸福夫妻(夫妻二人都感到幸福)的对数,求![]() 的期望(以样本的频率作为总体的概率).
的期望(以样本的频率作为总体的概率).