题目内容
【题目】已知椭圆C:![]() 过点
过点![]() ,且离心率为
,且离心率为![]()
(Ⅰ)求椭圆C的方程;
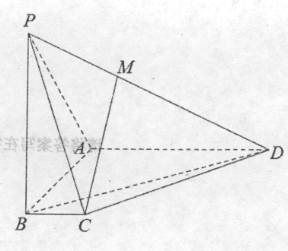
(Ⅱ)若过原点的直线![]() 与椭圆C交于P、Q两点,且在直线
与椭圆C交于P、Q两点,且在直线![]() 上存在点M,使得
上存在点M,使得![]() 为等边三角形,求直线
为等边三角形,求直线![]() 的方程。
的方程。
【答案】(Ⅰ)![]() (Ⅱ)y=0或y=
(Ⅱ)y=0或y=![]()
【解析】
(Ⅰ)列a,b,c的方程组求解即可求得方程;(Ⅱ)当![]() 的斜率k=0时符合题意;当
的斜率k=0时符合题意;当![]() 的斜率k
的斜率k![]() 0时,设直线
0时,设直线![]() 与椭圆联立,求得P,Q坐标,进而求得
与椭圆联立,求得P,Q坐标,进而求得![]() 设直线
设直线![]() 的中垂线方程:
的中垂线方程:![]() ,求其与
,求其与![]() 的交点M,由
的交点M,由![]() 为等边三角形,得到
为等边三角形,得到![]() 解方程求得k值即可
解方程求得k值即可
(Ⅰ)由题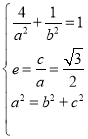 解得a=
解得a=![]() ,b=
,b=![]() ,c=
,c=![]() ,
,![]() 椭圆C的方程为
椭圆C的方程为![]()
(Ⅱ)由题,当![]() 的斜率k=0时,此时PQ=4
的斜率k=0时,此时PQ=4![]() 直线
直线![]() 与y轴的交点(0,
与y轴的交点(0,![]() 满足题意;
满足题意;
当![]() 的斜率k
的斜率k![]() 0时,设直线
0时,设直线![]() 与椭圆联立
与椭圆联立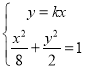 得
得![]() =8,
=8,![]() ,设P(
,设P(![]() ),则Q(
),则Q(![]() ),
),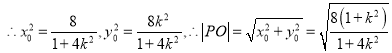 ,又PQ的垂直平分线方程为
,又PQ的垂直平分线方程为![]() 由
由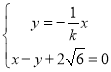 ,解得
,解得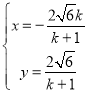 ,
,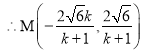 ,
,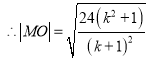 , ∵
, ∵![]() 为等边三角形
为等边三角形![]() 即
即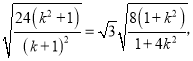 解得k=0(舍去),k=
解得k=0(舍去),k=![]() ,
,![]() 直线
直线![]() 的方程为y=
的方程为y=![]()
综上可知,直线![]() 的方程为y=0或y=
的方程为y=0或y=![]()

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目