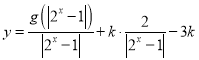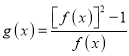Question

【题目】设函数 ．
（Ⅰ）求曲线 在点 处的切线方程；
（Ⅱ）若 对 恒成立，求实数 的取值范围；
（Ⅲ）求整数 的值，使函数 在区间 上有零点．

Answer 1

【答案】解：（Ⅰ） ，

∴ ，∴所求切线方程为 ，即

（Ⅱ）∵ ，对 恒成立，∴ ，

设 ，令 ，得 ，令 得 ，

∴ 在 上递减，在 上递增，

∴ ，∴

（Ⅲ）令 得 ，当 时， ，

∴ 的零点在 上，

令 得 或 ，∴ 在 上递增，又 在 上递减，

∴方程 仅有一解 ，且 ，

∵ ，

∴由零点存在的条件可得 ，∴

【解析】(I)根据导数的几何意义可求；
（II）函数含参恒成立问题，转化成求函数的最值问题，先分离参数a<,再构造函数,求导，确定函数的单调性，进而得到函数g(x)的最小值即可；
（III）函数的零点就是方程的解，也是两个函数的交点，因此先转化成两个函数，确定交点位置， F ( x ) 的零点在 ( 0 , + ∞ ) 上，再根据函数的单调性确定零点个数，后根据零点存在性定理确定零点位置即可。