题目内容
【题目】已知函数![]() .
.
(1)将函数![]() 写成分段函数的形式,并画出函数
写成分段函数的形式,并画出函数![]() 的大致图像;
的大致图像;
(2)求证:函数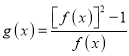 在
在![]() 上是增函数;
上是增函数;
(3)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有两个不相等的实数根,求实数
上有两个不相等的实数根,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析(2)见解析(3)![]()
【解析】试题分析:⑴由题意得到![]() ,画出其图象;
,画出其图象;
⑵先求出![]() ,运用定义法证明在
,运用定义法证明在![]() 上是增函数
上是增函数
⑶设![]() ,转化为关于
,转化为关于![]() 的方程
的方程![]() 在
在![]() 上仅有一个实根,结合图像与性质可得
上仅有一个实根,结合图像与性质可得![]() 或
或 ,即可求得结果
,即可求得结果
解析:(1)解:由题设得![]() ;
;
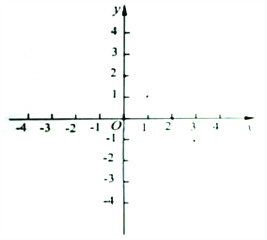
其图像如下图所示.
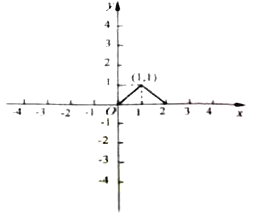
(2)证明:当![]() 时,
时, ![]() ,所以
,所以![]() ,
, ![]() .
.
任取![]() ,且
,且![]() ,则
,则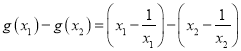
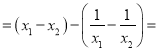

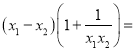
![]()
又![]() ,且
,且![]() ,
,
所以![]() ,
, ![]() ,
, ![]() 可得
可得![]() ,即
,即![]() ,
,
因此函数![]() 在
在![]() 上是增函数.
上是增函数.
(3)设![]() .由(1)得
.由(1)得![]() .
.
且![]() 时,方程
时,方程![]() 有两个不相等的实根.
有两个不相等的实根.
又关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有两个不相等的实根,
上有两个不相等的实根,
所以关于![]() 的方程
的方程![]() 在
在![]() 上仅有一个实根,且1不可为其根.
上仅有一个实根,且1不可为其根.
由于0不是方程![]() 的根,则关于
的根,则关于![]() 的方程
的方程![]() 在
在![]() 上仅有一个实根,且1不可为其根.
上仅有一个实根,且1不可为其根.
令![]() .
.
由其图像与性质可得![]() 或
或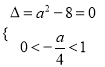 .
.
解得![]() 或
或![]() .
.
所以所求实数![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
【题目】某地区某中草药材的销售量与年份有关,下表是近五年的部分统计数据:
年份 | 2008 | 2010 | 2012 | 2014 | 2016 |
销售量(吨) | 114 | 115 | 116 | 116 | 114 |
(1)利用所给数据求年销售量![]() 与年份
与年份![]() 之间的回归直线方程
之间的回归直线方程![]() ;
;
(2)利用(1)中所求出的直线方程预测该地2018年的中草药的销售量.
参考公式: 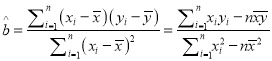 ,
, ![]() .
.
