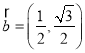题目内容
【题目】已知函数f（x）=|x+6|﹣|m﹣x|（m∈R）
（1）当m=3时，求不等式f（x）≥5的解集；
（2）若不等式f（x）≤7对任意实数x恒成立，求m的取值范围．
【答案】（1）
；（2）
.
【解析】
试题分析: 本题主要考查绝对值不等式、恒成立问题等基础知识，考查学生的分析问题解决问题的能力、转化能力、计算能力. 第一问，用零点分段法去掉绝对值，将绝对值不等式转化为不等式组求解；第二问，将不等式f（x）≤7对任意实数x恒成立，转化为
，利用不等式的性质求
的最大值，代入后解绝对值不等式得到
的取值范围.
试题解析：（1）当
时，
即
，
①当
时，得
，所以
；
②当
时，得
，即
，所以
；
③当
时，得
，成立，所以.
故不等式的解集为.
（Ⅱ）因为
＝
由题意得
，则
，
解得
,
故的取值范围是.
练习册系列答案
相关题目
