题目内容






⑴求椭圆
 的方程;
的方程;⑵设
 为椭圆上任意一点,以
为椭圆上任意一点,以 为圆心,
为圆心, 为半径作圆
为半径作圆 ,当圆
,当圆 与椭圆的右准线
与椭圆的右准线 有公共点时,求△
有公共点时,求△ 面积的最大值
面积的最大值(1)
 (2)
(2)
⑴因为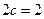 ,且
,且 ,所以
,所以 .……………………………2分
.……………………………2分
所以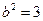 .……………………………………………………………………4分
.……………………………………………………………………4分
所以椭圆 的方程为
的方程为 .………………………………………6分
.………………………………………6分
⑵设点 的坐标为
的坐标为 ,则
,则 .
.
因为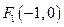 ,
, ,所以直线
,所以直线 的方程为
的方程为 .…………………8分
.…………………8分
由于圆 与
与 由公共点,所以
由公共点,所以 到
到 的距离
的距离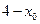 小于或等于圆的半径
小于或等于圆的半径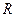 .
.
因为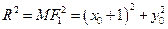 ,所以
,所以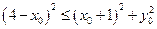 ,…………10分
,…………10分
即 .
.
又因为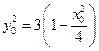 ,所以
,所以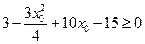 .………………12分
.………………12分
解得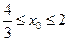 .…………………………………………………………14分
.…………………………………………………………14分
当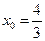 时,
时, ,所以
,所以 .…………16分
.…………16分
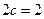 ,且
,且 ,所以
,所以 .……………………………2分
.……………………………2分所以
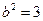 .……………………………………………………………………4分
.……………………………………………………………………4分所以椭圆
 的方程为
的方程为 .………………………………………6分
.………………………………………6分⑵设点
 的坐标为
的坐标为 ,则
,则 .
.因为
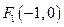 ,
, ,所以直线
,所以直线 的方程为
的方程为 .…………………8分
.…………………8分由于圆
 与
与 由公共点,所以
由公共点,所以 到
到 的距离
的距离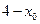 小于或等于圆的半径
小于或等于圆的半径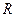 .
.因为
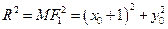 ,所以
,所以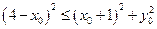 ,…………10分
,…………10分即
 .
.又因为
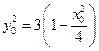 ,所以
,所以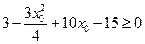 .………………12分
.………………12分解得
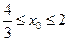 .…………………………………………………………14分
.…………………………………………………………14分当
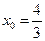 时,
时, ,所以
,所以 .…………16分
.…………16分
练习册系列答案
相关题目
 +
+ =1的长轴长为_________,短轴长为_________,焦点坐标为_________,顶点坐标为_________,离心率为__________.
=1的长轴长为_________,短轴长为_________,焦点坐标为_________,顶点坐标为_________,离心率为__________.



 到两点
到两点 ,写出椭圆
,写出椭圆 是(1)中所得椭圆上的动点,求线段
是(1)中所得椭圆上的动点,求线段 的中点
的中点 的轨迹方程;
的轨迹方程; 是椭圆
是椭圆 与椭圆相交于
与椭圆相交于 ,
, 两点,当直线
两点,当直线 ,
, 的斜率都存在,并记为
的斜率都存在,并记为 ,
, ,试探究
,试探究 的值是否与点
的值是否与点 的两个焦点为
的两个焦点为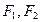 ,点
,点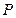 在椭圆
在椭圆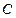 上,
上,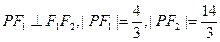 ,
,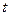 的取值范围,使得椭圆上有两个不同的点关于直线
的取值范围,使得椭圆上有两个不同的点关于直线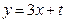 对称.
对称. 上任一点P,作椭圆C的右准线的垂线PH(H为垂足),延长PH到点Q,使|HQ|=λ|PH|(λ≥1)。当点P在椭圆C上运动时,点Q的轨迹的离心率的取值范围为( )
上任一点P,作椭圆C的右准线的垂线PH(H为垂足),延长PH到点Q,使|HQ|=λ|PH|(λ≥1)。当点P在椭圆C上运动时,点Q的轨迹的离心率的取值范围为( )




 在圆
在圆 上移动,点
上移动,点 在椭圆
在椭圆 上移动,求
上移动,求 的最大值.
的最大值. 的方程;
的方程; 在
在 轴上截距的取值范围;
轴上截距的取值范围; 面积的最大值
面积的最大值 ,
, 是椭圆上一点,且
是椭圆上一点,且 是
是 ,
, 的等差中项,则椭圆的标准方程是( ).
的等差中项,则椭圆的标准方程是( ).


