题目内容
【题目】如图,在三棱柱![]() 中,已知
中,已知![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1) 求证:![]() ;
;
(2) 求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)直棱柱的关系先证明![]() 和
和![]() 进而证明
进而证明![]() 平面
平面![]() ,从而得到
,从而得到![]() 即可.
即可.
(2)建立以![]() 为坐标原点,以
为坐标原点,以![]() ,
,![]() ,
,![]() 所在的直线分别为
所在的直线分别为![]() ,
,![]() ,
,![]() 轴的空间直角坐标系,再求出
轴的空间直角坐标系,再求出![]() 的向量与平面
的向量与平面![]() 的法向量求解即可.
的法向量求解即可.
解:(1)如图,连接![]() ,因为
,因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,
,![]() .
.
又![]() ,所以四边形
,所以四边形![]() 为正方形,所以
为正方形,所以![]() .
.
因为![]() ,所以
,所以![]() .又
.又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,所以,
,所以,![]() 平面
平面![]()
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]()
(2)解法1:在![]() 中,
中,![]() ,
,![]() ,
,![]() ,所以
,所以![]() .
.
又![]() 平面
平面![]() ,
,![]() ,所以三棱锥
,所以三棱锥![]() 的体积
的体积![]()
易知![]() ,
,![]() ,
,![]() ,
,
所以![]()
设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,则三棱锥
,则三棱锥![]() 的体积
的体积![]() ,
,
由等体积法可知![]() ,则
,则![]() ,解得
,解得![]() .
.
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,则
,则![]() ,
,
故直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]()
解法2:(2)由(1)知,![]() ,
,![]() ,
,![]() 两两垂直,以
两两垂直,以![]() 为坐标原点,以
为坐标原点,以![]() ,
,![]() ,
,![]() 所在的直线分别为
所在的直线分别为![]() ,
,![]() ,
,![]() 轴,建立如图所示的空间直角坐标系.因为
轴,建立如图所示的空间直角坐标系.因为![]() ,
,![]() .
.
所以![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]()
设平面![]() 的法向量为
的法向量为![]() ,则
,则 ,即
,即![]() ,
,
令![]() ,
,![]() ,所以
,所以![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
则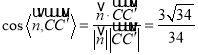
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,则
,则![]() ,
,
故直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]()


【题目】已知某芯片所获订单![]() (亿件)与生产精度
(亿件)与生产精度![]() (纳米)线性相关,该芯片的合格率
(纳米)线性相关,该芯片的合格率![]() 与生产精度
与生产精度![]() (纳米)也线性相关,并由下表中的5组数据得到,
(纳米)也线性相关,并由下表中的5组数据得到,![]() 与
与![]() 满足线性回归方程为:
满足线性回归方程为:![]() .
.
精度 | 16 | 14 | 10 | 7 | 3 |
订单 | 7 | 9 | 12 | 14.5 | 17.5 |
合格率 | 0.99 | 0.98 | 0.95 | 0.93 |
|
(1)求变量![]() 与
与![]() 的线性回归方程
的线性回归方程![]() ,并预测生产精度为1纳米时该芯片的订单(亿件);
,并预测生产精度为1纳米时该芯片的订单(亿件);
(2)若某工厂生产该芯片的精度为3纳米时,每件产品的合格率为![]() ,且各件产品是否合格相互独立.该芯片生产后成盒包装,每盒100件,每一盒产品在交付用户之前要对产品做检验,如检验出不合格品,则更换为合格品.现对一盒产品检验了10件,结果恰有一件不合格,已知每件产品的检验费用为
,且各件产品是否合格相互独立.该芯片生产后成盒包装,每盒100件,每一盒产品在交付用户之前要对产品做检验,如检验出不合格品,则更换为合格品.现对一盒产品检验了10件,结果恰有一件不合格,已知每件产品的检验费用为![]() 元,若有不合格品进入用户手中,则工厂要对每件不合格产品支付200元的赔偿费用.若不对该盒余下的产品检验,这一盒产品的检验费用与赔偿费用的和记为
元,若有不合格品进入用户手中,则工厂要对每件不合格产品支付200元的赔偿费用.若不对该盒余下的产品检验,这一盒产品的检验费用与赔偿费用的和记为![]() ,以
,以![]() 为决策依据,判断是否该对这盒余下的所有产品作检验?
为决策依据,判断是否该对这盒余下的所有产品作检验?
(参考公式: ,
,![]() )
)
(参考数据:![]() ;
;![]() )
)
【题目】某家庭为了解冬季用电量![]() (度)与气温
(度)与气温![]() 之间的关系,随机统计了某5天的用电量与当天气温,并制作了对照表,经过统计分析,发现气温在一定范围内时,用电量与气温具有线性相关关系:
之间的关系,随机统计了某5天的用电量与当天气温,并制作了对照表,经过统计分析,发现气温在一定范围内时,用电量与气温具有线性相关关系:
| 0 | 1 | 2 | 3 | 4 |
| 15 | 12 | 11 | 9 | 8 |
(1)求出用电量![]() 关于气温
关于气温![]() 的线性回归方程;
的线性回归方程;
(2)在这5天中随机抽取两天,求至少有一天用电量低于10(度)的概率.
(附:回归直线方程的斜率和截距的最小二乘法估计公式为 ,
,![]() )
)
