题目内容
【题目】解答
(1)在公比为2的等比数列{an}中,a2与a5的等差中项是9 ![]() .求a1的值;
.求a1的值;
(2)若函数y=a1sin( ![]() φ),0<φ<π的一部分图象如图所示,M(﹣1,a1),N(3,﹣a1)为图象上的两点,设∠MON=θ,其中O为坐标原点,0<θ<π,求cos(θ﹣φ)的值.
φ),0<φ<π的一部分图象如图所示,M(﹣1,a1),N(3,﹣a1)为图象上的两点,设∠MON=θ,其中O为坐标原点,0<θ<π,求cos(θ﹣φ)的值. 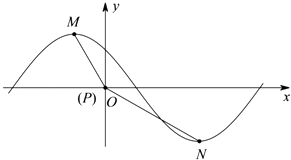
【答案】
(1)解:∵公比为2的等比数列{an}中,
a2与a5的等差中项是9 ![]() ,
,
![]() =
= ![]() =9
=9 ![]() ,
,
∴a2=2 ![]() =2a1,
=2a1,
∴a1= ![]() .
.
(2)解:若函数y=a1sin( ![]() φ)=
φ)= ![]() sin(
sin( ![]() φ),0<φ<π的一部分图象如图所示,M(﹣1,
φ),0<φ<π的一部分图象如图所示,M(﹣1, ![]() ),N(3,﹣
),N(3,﹣ ![]() )为图象上的两点,
)为图象上的两点,
结合五点法作图可得 ![]() (﹣1)+φ=
(﹣1)+φ= ![]() ,求得φ=
,求得φ= ![]() ,故y=
,故y= ![]() sin(
sin( ![]() ).
).
△MON中,由∠MON=θ,其中O为坐标原点,利用余弦定理可得cosθ= ![]() =
= ![]() =﹣
=﹣ ![]() ,
,
再结合0<θ<π,可得θ= ![]() ,
,
求cos(θ﹣φ)=cos( ![]() ﹣
﹣ ![]() )=cos
)=cos ![]() =cos(
=cos( ![]() ﹣
﹣ ![]() )=cos
)=cos ![]() cos
cos ![]() +sin
+sin ![]() sin
sin ![]() =
= ![]()
【解析】(1)由条件利用等差中项、等比数列的定义,求得a1的值.(2)由五点法作图求出φ的值,可得函数的解析式,△MON中,再利用余弦定理求得cosθ的值,再利用两角差的余弦公公式,求得cos(θ﹣φ)的值.
【考点精析】本题主要考查了两角和与差的余弦公式的相关知识点,需要掌握两角和与差的余弦公式:![]() 才能正确解答此题.
才能正确解答此题.

练习册系列答案
相关题目