题目内容
【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AC⊥AB,AD⊥DC,∠DAC=60°,PA=AC=2,AB=1. 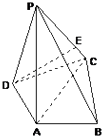
(1)求二面角A﹣PB﹣C的余弦值.
(2)在线段CP上是否存在一点E,使得DE⊥PB,若存在,求线段CE的长度,不存在,说明理由.
【答案】
(1)解:以A为坐标原点,以AB,AC,AP为坐标轴建立空间直角坐标系,
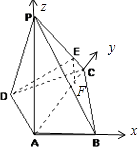
则P(0,0,2),A(0,0,0),B(1,0,0),C(0,2,0),D(﹣ ![]() ,
, ![]() ,0).
,0).
∴ ![]() =(0,2,﹣2),
=(0,2,﹣2), ![]() =(1,0,﹣2),
=(1,0,﹣2), ![]() =(0,2,0).
=(0,2,0).
显然 ![]() =(0,2,0)为平面PAB的法向量.
=(0,2,0)为平面PAB的法向量.
设平面PBC的法向量为 ![]() =(x,y,z),
=(x,y,z),
则 ![]() ,
, ![]() =0,
=0,
∴ ![]() ,令z=1,得
,令z=1,得 ![]() =(2,1,1).
=(2,1,1).
∴ ![]() =2,|
=2,| ![]() |=
|= ![]() ,|
,| ![]() |=2.
|=2.
∴cos< ![]() ,
, ![]() >=
>= 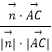 =
= ![]() .
.
∴二面角A﹣PB﹣C的余弦值为 ![]()
(2)解:过E作EF⊥AC于F,∴EF∥PA,∴EF=FC.
设EF=h,则E(0,2﹣h,h).
∴ ![]() =(
=( ![]() ,
, ![]() -h,h),
-h,h), ![]() =(1,0,﹣2).
=(1,0,﹣2).
∵DE⊥PB,∴ ![]() =
= ![]() ﹣2h=0,解得h=
﹣2h=0,解得h= ![]() .
.
∴CE= ![]() h=
h= ![]() .
.
【解析】(1)以A为原点建立空间直角坐标系,求出平面PAB和平面PBC的法向量,则法向量的夹角与二面角的大小相等或互补;(2)作EF⊥AC于F,则EF=FC,设EF=h,求出E点坐标得出 ![]() 的坐标,令
的坐标,令 ![]() =0解出h,从而得出CE.
=0解出h,从而得出CE.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案
相关题目