题目内容
【题目】祖暅是我国古代的伟大科学家,他在5世纪末提出祖暅:“幂势即同,则积不容异”,意思是:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意一个平面所截,若截面面积都相等,则这两个几何体的体积相等. 祖暅原理常用来由已知几何体的体积推导未知几何体的体积,例如由圆锥和圆柱的的体积推导半球体的体积,其示意图如图所示,其中图(1)是一个半径为R的半球体,图(2)是从圆柱中挖去一个圆锥所得到的几何体. (圆柱和圆锥的底面半径和高均为R)

利用类似的方法,可以计算抛物体的体积:在x-O-y坐标系中,设抛物线C的方程为y=1-x2 (-1![]() x
x![]() 1),将曲线C围绕y轴旋转,得到的旋转体称为抛物体. 利用祖暅原理可计算得该抛物体的体积为_________.
1),将曲线C围绕y轴旋转,得到的旋转体称为抛物体. 利用祖暅原理可计算得该抛物体的体积为_________.
【答案】![]()
【解析】分析:构造直三棱柱,证明二者截面面积相等,从而求出三棱柱体积,即可得到抛物体的体积.
详解:构造如图所示的直三棱柱,高设为x,底面两个直边长为2,1
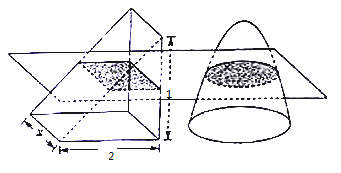
若底面积相等得到:![]() ,
,![]()
下面说明截面面积相等,设截面距底面为t,矩形截面长为a,圆形截面半径为r,
由左图得到,![]() ,∴
,∴![]() ,∴截面面积为
,∴截面面积为![]()
由右图得到,![]() (坐标系中易得),∴
(坐标系中易得),∴![]() ,∴截面面积为
,∴截面面积为![]()
∴二者截面面积相等,∴体积相等.
∴抛物体的体积为![]() .
.

练习册系列答案
相关题目