题目内容
【题目】如图,在四棱锥![]() 中,
中,![]()
![]() 平面
平面![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是线段
是线段![]() 的中点.
的中点.
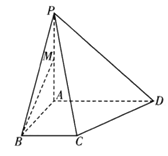
(1)证明:![]() 平面
平面![]()
![]()
(2)当![]() 为何值时,四棱锥
为何值时,四棱锥![]() 的体积最大?并求此最大值
的体积最大?并求此最大值
【答案】(1)见解析(2)当PA=4时,体积最大值为16.
【解析】
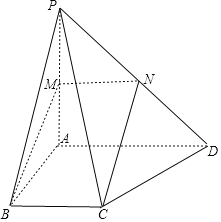
(1)取PD中点N,易证MNCB为平行四边形,进而得BM,CN平行,得证;
(2)设PA=x(0![]() ),把体积表示为关于x的函数,借助不等式求得最大值.
),把体积表示为关于x的函数,借助不等式求得最大值.
(1)取PD中点N,连接MN,CN,
∵M是AP的中点,
∴MN∥AD且MN![]() ,
,
∵AD∥BC,AD=2BC,
∴MN∥BC,MN=BC,
∴四边形MNCB是平行四边形,
∴MB∥CN,
又BM![]() 平面PCD,CN平面PCD,
平面PCD,CN平面PCD,
∴BM∥平面PCD;
(2)设PA=x(0<x<4![]() ),
),
∵PA⊥平面ABCD,
∴PA⊥AB,
∵![]() ,
,
∴AB![]() ,
,
又∵AB⊥AD,AD=2BC=4,
∴VP﹣ABCD![]()
![]()
![]()
![]()
=16,
当且仅当x![]() ,即x=4时取等号,
,即x=4时取等号,
故当PA=4时,四棱锥P﹣ABCD的体积最大,最大值为16.

练习册系列答案
相关题目
【题目】近期中央电视台播出的《中国诗词大会》火遍全国,下面是组委会在选拔赛时随机抽取的100名选手的成绩,按成绩分组,得到的频率分布表如下所示.
题号 | 分组 | 频数 | 频率 |
第1组 |
| 0.100 | |
第2组 |
| ① | |
第3组 |
| 20 | ② |
第4组 |
| 20 | 0.200 |
第5组 |
| 10 | 0.100 |
第6组 |
| 100 | 1.00 |
(1)请先求出频率分布表中①、②位置的相应数据,再完成如下的频率分布直方图;

(2)组委会决定在5名(其中第3组2名,第4组2名,第5组1名)选手中随机抽取2名选接受![]() 考官进行面试,求第4组至少有1名选手被考官
考官进行面试,求第4组至少有1名选手被考官![]() 面试的概率.
面试的概率.




