题目内容
【题目】已知椭圆
的离心率为
，焦点分别为
，点
是椭圆
上的点，
面积的最大值是
．
（Ⅰ）求椭圆的方程；
（Ⅱ）设直线
与椭圆交于
两点，点
是椭圆上的点，
是坐标原点，若
判定四边形
的面积是否为定值？若为定值，求出定值；如果不是，请说明理由．
【答案】（Ⅰ） 
（Ⅱ）见解析
【解析】
（Ⅰ）由题意得到
的方程组，求出
的值，即可得出椭圆方程；
（Ⅱ）当直线
的斜率不存在时，易求出四边形
的面积；当直线的斜率存在时，设直线方程是
，联立直线与椭圆方程，结合判别式和韦达定理，可表示出弦长
，再求出点
到直线
的距离，根据
和点
在曲线
上，求出
的关系式，
最后根据
，即可得出结果.
解：（Ⅰ）由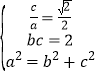
解得
得椭圆的方程为.
（Ⅱ）当直线的斜率不存在时，直线的方程为
或
，此时四边形的面积为
．
当直线的斜率存在时，设直线方程是，联立椭圆方程
，
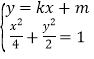
点到直线的距离是
由
得
因为点在曲线上，所以有
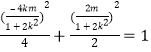整理得
由题意四边形为平行四边形，所以四边形的面积为
由得
, 故四边形的面积是定值，其定值为．
练习册系列答案
相关题目
