题目内容
14.已知抛物线y2=4x的焦点为F,过点(0,3)的直线与抛物线交于A、B两点,线段AB的垂直平分线交x轴于点D,若|AF|+|BF|=6,则点D的横坐标为( )| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
分析 设AB的中点为H,求出准线方程,设A,B,H在准线上的射影分别为A',B',H',运用抛物线的定义可得H的横坐标为2,设出直线AB的方程,联立抛物线方程,运用韦达定理和判别式大于0,求得k的范围,由中点坐标公式解得k=-2,再求直线AB的中垂线方程,令y=0,即可得到所求值.
解答  解:设AB的中点为H,
解:设AB的中点为H,
抛物线y2=4x的焦点为F(1,0),准线为x=-1,
设A,B,H在准线上的射影分别为A',B',H',
则|HH'|=$\frac{1}{2}$(|AA'|+|BB'|),
由抛物线的定义可得,
|AF|=|AA'|,|BF|=|BB'|,
|AF|+|BF|=6,即为|AA'|+|BB'|=6,
|HH'|=$\frac{1}{2}$×6=3,
即有H的横坐标为2,
设直线AB:y=kx+3,
代入抛物线方程,可得k2x2+(6k-4)x+9=0,
即有判别式(6k-4)2-36k2>0,解得k<$\frac{1}{3}$且k≠0,
又x1+x2=$\frac{4-6k}{{k}^{2}}$=4,
解得k=-2或$\frac{1}{2}$(舍去),
则直线AB:y=-2x+3,
AB的中点为(2,-1),
AB的中垂线方程为y+1=$\frac{1}{2}$(x-2),
令y=0,解得x=4,
故选:B.
点评 本题考查抛物线的定义、方程和性质,主要考查抛物线的准线方程的运用,同时考查直线和抛物线方程联立,运用判别式和韦达定理,考查两直线垂直的条件和中点坐标公式的运用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.如图,在矩形ABCD中,已知AB=2,BC=1,若在矩形ABCD中任取一点P,则点P满足|AP|≤1的概率为( )


| A. | $\frac{π}{8}$ | B. | $\frac{π}{16}$ | C. | $\frac{π}{32}$ | D. | $\frac{π}{64}$ |
3.在△ABC中,若A=60°,B=45°,a=3$\sqrt{2}$,则b=( )
| A. | 4$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
4.若f(x)=sin$\frac{π}{3}$-cosx,则f′(a)等于( )
| A. | sinα | B. | cosα | C. | sin$\frac{π}{3}$+cosα | D. | cos$\frac{π}{3}$+sinα |
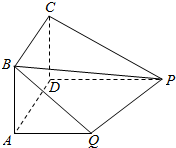 如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=$\frac{1}{2}$PD=1.
如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=$\frac{1}{2}$PD=1.