题目内容
分别指出由下列命题构成的“p q”、“p
q”、“p q”、“
q”、“ p”形式的命题的真假.
p”形式的命题的真假.
(1)p:4∈{2,3},q:2∈{2,3};
(2)p:1是奇数,q:1是质数;
(3)p:0∈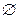 ,q:{x|x2-3x-5<0}
,q:{x|x2-3x-5<0}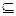 R;
R;
(4)p:5≤5,q:27不是质数;
(5)p:不等式x2+2x-8<0的解集是{x|-4<x<2},
q:不等式x2+2x-8<0的解集是{x|x<-4或x>2}.
 q”、“p
q”、“p q”、“
q”、“ p”形式的命题的真假.
p”形式的命题的真假.(1)p:4∈{2,3},q:2∈{2,3};
(2)p:1是奇数,q:1是质数;
(3)p:0∈
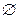 ,q:{x|x2-3x-5<0}
,q:{x|x2-3x-5<0}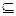 R;
R;(4)p:5≤5,q:27不是质数;
(5)p:不等式x2+2x-8<0的解集是{x|-4<x<2},
q:不等式x2+2x-8<0的解集是{x|x<-4或x>2}.
(1)p q为真,p
q为真,p q为假,
q为假, P为真.
P为真.
(2)p q为真,p
q为真,p q为假,
q为假, p为假.
p为假.
(3) p q为真命题,p
q为真命题,p q为假命题,
q为假命题, p为真命题.
p为真命题.
(4)p q为真命题,p
q为真命题,p q为真命题,
q为真命题, p为假命题.
p为假命题.
(5)p q为真,p
q为真,p q为假,
q为假, p为假.
p为假.
 q为真,p
q为真,p q为假,
q为假, P为真.
P为真.(2)p
 q为真,p
q为真,p q为假,
q为假, p为假.
p为假.(3) p
 q为真命题,p
q为真命题,p q为假命题,
q为假命题, p为真命题.
p为真命题.(4)p
 q为真命题,p
q为真命题,p q为真命题,
q为真命题, p为假命题.
p为假命题.(5)p
 q为真,p
q为真,p q为假,
q为假, p为假.
p为假.(1)∵p是假命题,q是真命题,∴p q为真,p
q为真,p q为假,
q为假, P为真.
P为真.
(2)∵1是奇数,∴p是真命题,
又∵1不是质数,∴q是假命题,因此p q为真,p
q为真,p q为假,
q为假, p为假.
p为假.
(3)∵0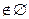 ,∴p为假命题,
,∴p为假命题,
又∵x2-3x-5<0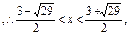
∴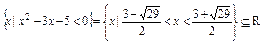 成立.
成立.
∴q为真命题.∴p q为真命题,p
q为真命题,p q为假命题,
q为假命题, p为真命题.
p为真命题.
(4)显然p:5≤5为真命题,q:27不是质数为真命题,
∴p q为真命题,p
q为真命题,p q为真命题,
q为真命题, p为假命题.
p为假命题.
(5)∵x2+2x-8<0, ∴(x+4)(x-2)<0.
即-4<x<2,∴x2+2x-8<0的解集为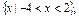 ∴命题p为真,q为假.
∴命题p为真,q为假.
∴p q为真,p
q为真,p q为假,
q为假, p为假.
p为假.
 q为真,p
q为真,p q为假,
q为假, P为真.
P为真.(2)∵1是奇数,∴p是真命题,
又∵1不是质数,∴q是假命题,因此p
 q为真,p
q为真,p q为假,
q为假, p为假.
p为假.(3)∵0
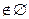 ,∴p为假命题,
,∴p为假命题,又∵x2-3x-5<0
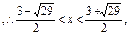
∴
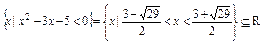 成立.
成立.∴q为真命题.∴p
 q为真命题,p
q为真命题,p q为假命题,
q为假命题, p为真命题.
p为真命题.(4)显然p:5≤5为真命题,q:27不是质数为真命题,
∴p
 q为真命题,p
q为真命题,p q为真命题,
q为真命题, p为假命题.
p为假命题.(5)∵x2+2x-8<0, ∴(x+4)(x-2)<0.
即-4<x<2,∴x2+2x-8<0的解集为
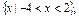 ∴命题p为真,q为假.
∴命题p为真,q为假.∴p
 q为真,p
q为真,p q为假,
q为假, p为假.
p为假.
练习册系列答案
相关题目
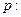 函数
函数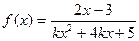 的定义域为
的定义域为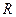 ;
;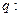 关于
关于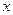 的方程
的方程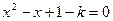 的两个实根
的两个实根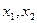 满足
满足 。
。 或
或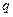 ”与命题“
”与命题“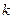 的取值范围
的取值范围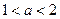 ,设命题
,设命题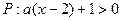 ,命题
,命题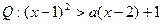 ,非P∨非Q是假命题,求
,非P∨非Q是假命题,求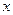 的集合。
的集合。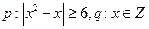 且“
且“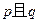 ”与“非
”与“非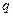 ”同时为假命题,求
”同时为假命题,求 的值。
的值。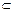 平面β,有下列四个命题:①
平面β,有下列四个命题:①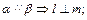
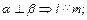 ③
③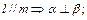 ④
④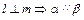 。其中真命题是
。其中真命题是 ,使
,使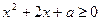 ”为真命题,则实数a的取值范围是( )
”为真命题,则实数a的取值范围是( )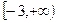
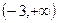
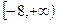

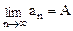 ,
,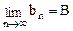 ,则
,则 (
( )
)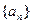 ,
,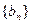 的极限都不存在,则
的极限都不存在,则 的极限也不存在
的极限也不存在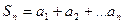 ,若数列
,若数列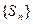 的极限也存在
的极限也存在