题目内容
若a、b、c∈R，写出命题“若ac＜0，则ax2+bx+c=0有两个不相等的实数根”的逆命题、否命题、逆否命题，并判断这三个命题的真假
同解析
[解题思路]：认清命题的条件p和结论q，然后按定义写出逆命题、否命题、逆否命题，最后判断真假
逆命题：若ax2+bx+c=0（a、b、c∈R）有两个不相等的实数根，则ac＜0；是假命题，如当a=1，b=－3，c=2时，方程x2－3x+2=0有两个不等实根x1=1，x2=2，但ac=2＞0
否命题：若ac≥0，则方程ax2+bx+c=0（a、b、c∈R）没有两个不相等的实数根；是假命题. 这是因为它和逆命题互为逆否命题，而逆命题是假命题
逆否命题：若ax2+bx+c=0（a、b、c∈R）没有两个不相等的实数根，则ac≥0；是真命题. 因为原命题是真命题，它与原命题等价
逆命题：若ax2+bx+c=0（a、b、c∈R）有两个不相等的实数根，则ac＜0；是假命题，如当a=1，b=－3，c=2时，方程x2－3x+2=0有两个不等实根x1=1，x2=2，但ac=2＞0
否命题：若ac≥0，则方程ax2+bx+c=0（a、b、c∈R）没有两个不相等的实数根；是假命题. 这是因为它和逆命题互为逆否命题，而逆命题是假命题
逆否命题：若ax2+bx+c=0（a、b、c∈R）没有两个不相等的实数根，则ac≥0；是真命题. 因为原命题是真命题，它与原命题等价
练习册系列答案
同步练习河南大学出版社系列答案
同步练习西南师范大学出版社系列答案
补充习题江苏系列答案
学练快车道口算心算速算天天练系列答案
相关题目
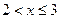
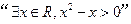的否定是“
”；
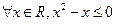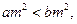则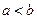
”的逆命题为真；
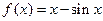（x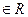
）有3个零点；
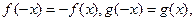且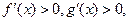x>0时,
则x<0时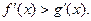
q”、“p
q”、“
p”形式的命题的真假.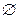
，q：{x|x2-3x-5＜0}
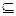R；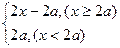
,函数y>1恒成立, 若p∧q为假,p∨q为真,求a的取值范围
；命题Q：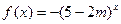
是增函数，若P或Q为真命题，P且Q为假命题，则实数m的取值范围是 。
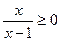的解集为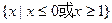
”；命题q：“不等式
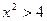的解集为
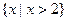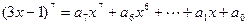”，则 （ ）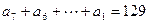
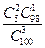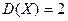，则
；
；
，则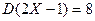
．