题目内容
如图,直线l:y=x+b与抛物线x2=4y相切于点A.
(1)求实数b的值;
(2)若过抛物线的焦点且平行于直线l的直线l1交抛物线于B,C两点,求△ABC的面积.
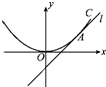
(1)求实数b的值;
(2)若过抛物线的焦点且平行于直线l的直线l1交抛物线于B,C两点,求△ABC的面积.

(1)由直线l:y=x+b与抛物线x2=4y,消去y,
可$\end{array}\right.$得x2=4(x+b),即x2-4x-4b=0…(2分)
∵直线l与抛物线相切,
∴△=16+16b=0,即b=-1…(5分)
(2)∵抛物线的焦点为(0,1),
∴由题意可知直线l1的方程为y=x+1…(7分)
由
得x2-4x-4=0…(8分)
设B(x1,y1),C(x2,y2),则x1+x2=4,x1x2=-4,
∴|BC|=
•|x1-x2|=
•
=8…(10分)
由(1)得点的坐标为A(2,1)…(11分)
∴点A到直线l1的距离d=
=
…(12分)
∴S△ABC=
|BC|d=4
…(13分)
可$\end{array}\right.$得x2=4(x+b),即x2-4x-4b=0…(2分)
∵直线l与抛物线相切,
∴△=16+16b=0,即b=-1…(5分)
(2)∵抛物线的焦点为(0,1),
∴由题意可知直线l1的方程为y=x+1…(7分)
由
|
设B(x1,y1),C(x2,y2),则x1+x2=4,x1x2=-4,
∴|BC|=
| 2 |
| 2 |
| 16+16 |
由(1)得点的坐标为A(2,1)…(11分)
∴点A到直线l1的距离d=
| |2-1+1| | ||
|
| 2 |
∴S△ABC=
| 1 |
| 2 |
| 2 |

练习册系列答案
相关题目