题目内容
⑴已知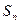 为等差数列
为等差数列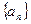 的前
的前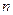 项和,
项和,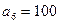 ,则
,则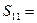 ;
;
⑵已知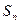 为等差数列
为等差数列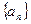 的前
的前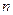 项和,
项和,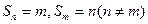 ,则
,则 .
.
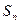 为等差数列
为等差数列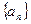 的前
的前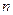 项和,
项和,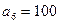 ,则
,则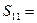 ;
;⑵已知
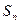 为等差数列
为等差数列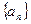 的前
的前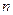 项和,
项和,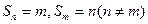 ,则
,则 .
.⑴1100,⑵

利用等差数列的有关性质求解.⑴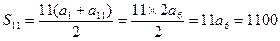 ;
;
⑵方法1:令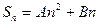 ,则
,则
 .
.

 ,
,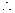
 ,
,
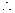
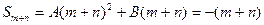 ;
;
方法2:不妨设
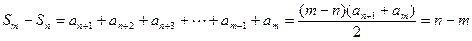 .
.
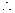
 ,
,
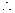
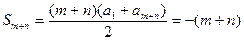 ;
;
方法3:
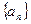 是等差数列,
是等差数列,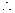
 为等差数列
为等差数列
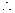
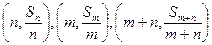 三点共线.
三点共线.
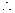
 .
.
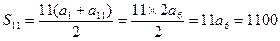 ;
;⑵方法1:令
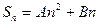 ,则
,则 .
.
 ,
,
 ,
,
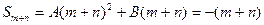 ;
;方法2:不妨设

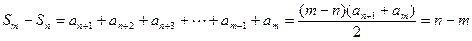 .
.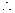
 ,
,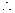
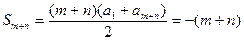 ;
;方法3:

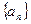 是等差数列,
是等差数列,
 为等差数列
为等差数列
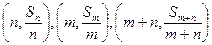 三点共线.
三点共线.
 .
.
练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
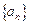 的前
的前 项和为
项和为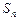 ,已知
,已知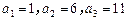 ,且
,且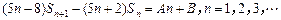 ,
,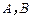 为常数.
为常数.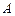 与
与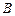 的值;
的值;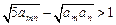 对任何正整数
对任何正整数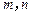 都成立.
都成立. 的定义域为
的定义域为 ,且对任意的正实数x,y有:
,且对任意的正实数x,y有: 且
且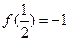 .
.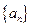 满足:
满足: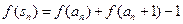 其中
其中 为数列
为数列
 成立?若存在,求出M的取值范围;若不存在,请说明理由.
成立?若存在,求出M的取值范围;若不存在,请说明理由.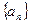 中,
中,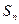 是其前
是其前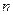 项和,且
项和,且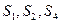 成等比数列.
成等比数列.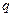 ;
;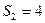 ,求等差数列
,求等差数列 向三次曲线
向三次曲线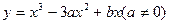 引切线,切于不同于点
引切线,切于不同于点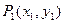 ,再由
,再由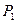 引此曲线的切线,切于不同于
引此曲线的切线,切于不同于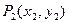 ,如此继续地作下去,……,得到点列
,如此继续地作下去,……,得到点列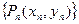 ,试回答下列问题: ⑴求
,试回答下列问题: ⑴求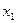 ; (2)求
; (2)求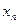 与
与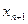 的关系式;
的关系式; 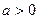 ,求证:当
,求证:当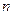 为正偶数时,
为正偶数时,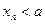 ;当
;当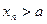 .
.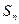 为等差数列
为等差数列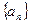 的前
的前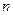 项和,
项和,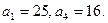
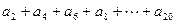 的值;
的值;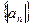 的前
的前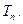
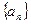 为等差数列,
为等差数列, (
(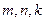 互不相等),求
互不相等),求 .
.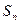 是数列
是数列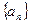 的前
的前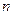 项和,
项和, 则
则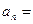 .
.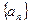 中,公差
中,公差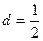 ,前
,前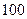 项的和
项的和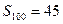 ,
,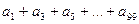 =_____________
=_____________