题目内容
已知:公差不为零的等差数列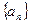 中,
中,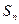 是其前
是其前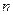 项和,且
项和,且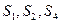 成等比数列.
成等比数列.
⑴求数列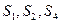 的公比
的公比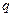 ;
;
⑵若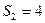 ,求等差数列
,求等差数列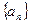 的通项公式.
的通项公式.
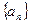 中,
中,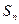 是其前
是其前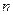 项和,且
项和,且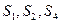 成等比数列.
成等比数列.⑴求数列
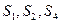 的公比
的公比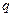 ;
;⑵若
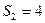 ,求等差数列
,求等差数列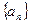 的通项公式.
的通项公式. ⑴4,⑵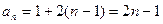
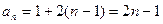
⑴设等差数列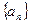 的公差为
的公差为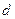 ,则
,则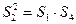 ,即
,即 (2分)
(2分)
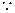
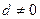 ,
,
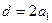 ,(5分)
,(5分) 
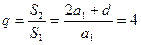 (7分)
(7分)
⑵由⑴知,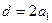 , ①
, ① 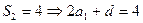 ② (9分)
② (9分)
由①②解得,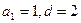 ,
,
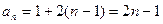 . (14分)
. (14分)
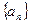 的公差为
的公差为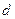 ,则
,则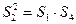 ,即
,即 (2分)
(2分)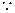
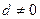 ,
,
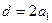 ,(5分)
,(5分) 
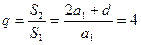 (7分)
(7分)⑵由⑴知,
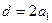 , ①
, ① 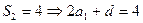 ② (9分)
② (9分)由①②解得,
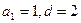 ,
,
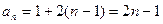 . (14分)
. (14分)
练习册系列答案
相关题目
 (an-1),数列{bn}的通项公式为bn=4n+3;
(an-1),数列{bn}的通项公式为bn=4n+3;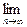
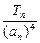

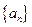 首项
首项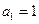 ,前
,前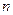 项和
项和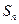 与
与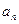 之间满足
之间满足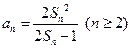
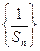 是等差数列 (2)求数列
是等差数列 (2)求数列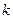 ,使
,使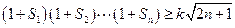 对于一切
对于一切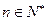 都成立,求
都成立,求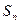 为等差数列
为等差数列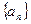 的前
的前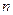 项和,
项和,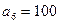 ,则
,则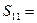 ;
;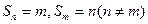 ,则
,则 .
.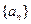 中,
中,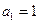 ,
,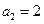 ,且
,且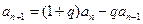 (
(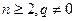 )。
)。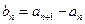 (
(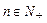 ),求数列
),求数列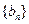 的通项公式;
的通项公式;
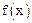 的单调区间;
的单调区间;
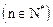 上的最小值为
上的最小值为 令
令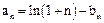 ;
;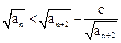 恒成立,求实数c的取值范围;
恒成立,求实数c的取值范围;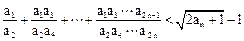 。
。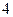 个实数
个实数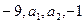 成等差数列,
成等差数列,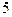 个实数
个实数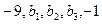 成等比数列,
成等比数列,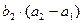 .
.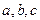 成等比数列,
成等比数列,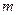 是
是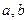 的等差中项,
的等差中项,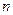 是
是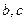 的等差中项,则
的等差中项,则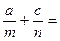 .
.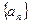 中,
中,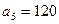 ,则
,则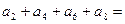 .
.