题目内容
设数列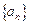 的前
的前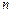 项和为
项和为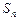 ,已知
,已知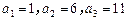 ,且
,且
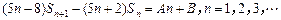 ,
,
其中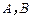 为常数.
为常数.
(Ⅰ)求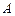 与
与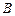 的值;
的值;
(Ⅱ)证明:数列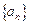 为等差数列;
为等差数列;
(Ⅲ)证明:不等式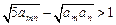 对任何正整数
对任何正整数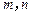 都成立.
都成立.
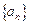 的前
的前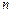 项和为
项和为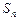 ,已知
,已知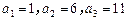 ,且
,且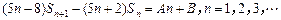 ,
,其中
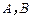 为常数.
为常数.(Ⅰ)求
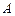 与
与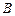 的值;
的值;(Ⅱ)证明:数列
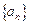 为等差数列;
为等差数列;(Ⅲ)证明:不等式
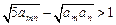 对任何正整数
对任何正整数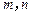 都成立.
都成立.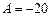 ,
,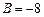 .
.解:(Ⅰ)由已知,得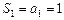 ,
,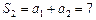 ,
,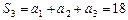 .
.
由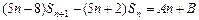 ,知
,知
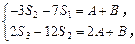 即
即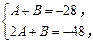
解得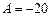 ,
,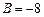 .
.
(Ⅱ)方法1
由(Ⅰ),得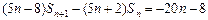 , ①
, ①
所以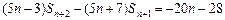 . ②
. ②
②-①,得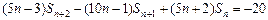 , ③
, ③
所以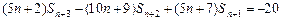 . ④
. ④
④-③,得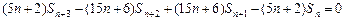 .
.
因为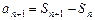 ,
,
所以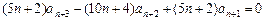 .
.
又因为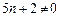 ,
,
所以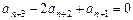 ,
,
即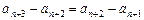 ,
,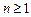 .
.
所以数列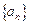 为等差数列.
为等差数列.
方法2
由已知,得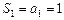 ,
,
又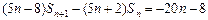 ,且
,且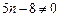 ,
,
所以数列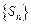 是唯一确定的,因而数列
是唯一确定的,因而数列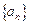 是唯一确定的.
是唯一确定的.
设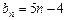 ,则数列
,则数列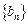 为等差数列,前
为等差数列,前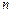 项和
项和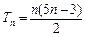 .
.
于是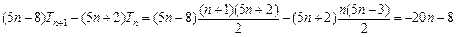 ,
,
由唯一性得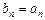 ,即数列
,即数列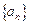 为等差数列.
为等差数列.
(Ⅲ)由(Ⅱ)可知,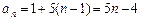 .
.
要证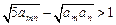 ,
,
只要证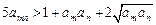 .
.
因为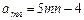 ,
,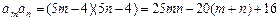 ,
,
故只要证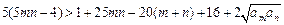 ,
,
即只要证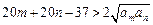 .
.
因为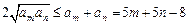
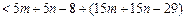
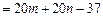 ,
,
所以命题得证.
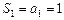 ,
,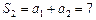 ,
,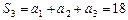 .
.由
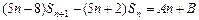 ,知
,知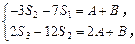 即
即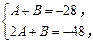
解得
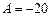 ,
,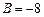 .
.(Ⅱ)方法1
由(Ⅰ),得
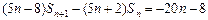 , ①
, ①所以
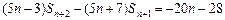 . ②
. ②②-①,得
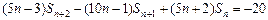 , ③
, ③所以
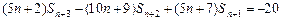 . ④
. ④④-③,得
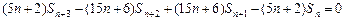 .
.因为
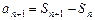 ,
,所以
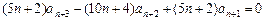 .
.又因为
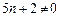 ,
,所以
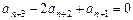 ,
,即
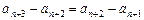 ,
,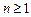 .
.所以数列
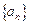 为等差数列.
为等差数列.方法2
由已知,得
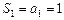 ,
,又
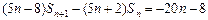 ,且
,且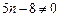 ,
,所以数列
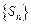 是唯一确定的,因而数列
是唯一确定的,因而数列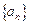 是唯一确定的.
是唯一确定的.设
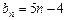 ,则数列
,则数列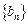 为等差数列,前
为等差数列,前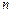 项和
项和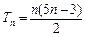 .
.于是
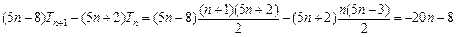 ,
,由唯一性得
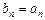 ,即数列
,即数列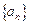 为等差数列.
为等差数列.(Ⅲ)由(Ⅱ)可知,
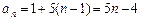 .
.要证
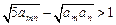 ,
,只要证
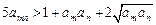 .
.因为
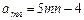 ,
,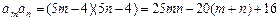 ,
,故只要证
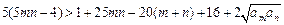 ,
,即只要证
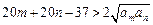 .
.因为
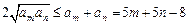
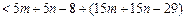
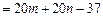 ,
,所以命题得证.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
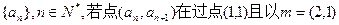 为方向向量的直线上,
为方向向量的直线上,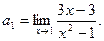 (I)求数列
(I)求数列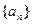 的通项公式;(II)求证:
的通项公式;(II)求证: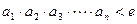 (其中e为自然对数的底数);
(其中e为自然对数的底数);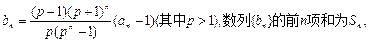
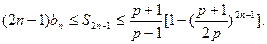
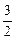 (an-1),数列{bn}的通项公式为bn=4n+3;
(an-1),数列{bn}的通项公式为bn=4n+3;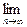
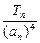

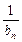 )(其中a>0且a≠1),记Sn是数列{an}的前n项和,试比较Sn与
)(其中a>0且a≠1),记Sn是数列{an}的前n项和,试比较Sn与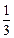 logabn+1的大小,并证明你的结论.
logabn+1的大小,并证明你的结论.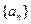 中,
中,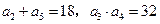 ,并且
,并且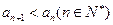 (1)求
(1)求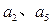 以及数列
以及数列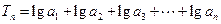 ,求当
,求当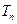 最大时
最大时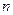 的值.
的值.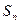 为等差数列
为等差数列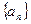 的前
的前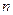 项和,
项和,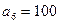 ,则
,则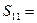 ;
;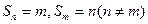 ,则
,则 .
.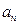 表示第
表示第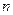 排的座位数吗?第10排能坐多少个人?
排的座位数吗?第10排能坐多少个人?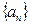 的前n项和为
的前n项和为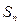 ,对于任意正整数n,都有等式:
,对于任意正整数n,都有等式: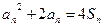 成立,求
成立,求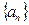 的通项an.
的通项an.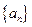 前项
前项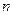 和为
和为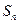 ,且
,且