题目内容
2.已知数列 {an}满足 a1=1,an-an+1=nanan+1(n∈N*),则 an=$\frac{2}{{n}^{2}-n+2}$.分析 通过an-an+1=nanan+1(n∈N*),可得$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$=n,并项相加可得$\frac{1}{{a}_{n}}$=$\frac{{n}^{2}-n+2}{2}$,进而可得结论.
解答 解:∵an-an+1=nanan+1(n∈N*),
∴$\frac{{a}_{n}-{a}_{n+1}}{{a}_{n}{a}_{n+1}}$=$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$=n,
∴$\frac{1}{{a}_{n}}$=($\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{n-1}}$)+($\frac{1}{{a}_{n-1}}$-$\frac{1}{{a}_{n-2}}$)+…+($\frac{1}{{a}_{3}}$-$\frac{1}{{a}_{2}}$)+($\frac{1}{{a}_{2}}$-$\frac{1}{{a}_{1}}$)+$\frac{1}{{a}_{1}}$
=(n-1)+(n-2)+…+3+2+1+$\frac{1}{{a}_{1}}$
=$\frac{(n-1)(n-1+1)}{2}$+1
=$\frac{{n}^{2}-n+2}{2}$,
∴an=$\frac{2}{{n}^{2}-n+2}$,
故答案为:$\frac{2}{{n}^{2}-n+2}$.
点评 本题考查求数列的通项,利用并项相加法是解决本题的关键,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
13. 如图是利用斜二测画法画出的△ABO的直观图,已知O′B′=4,且△ABO的面积为16,过A′作A′C′⊥x′轴,则A′C′的长为( )
如图是利用斜二测画法画出的△ABO的直观图,已知O′B′=4,且△ABO的面积为16,过A′作A′C′⊥x′轴,则A′C′的长为( )
 如图是利用斜二测画法画出的△ABO的直观图,已知O′B′=4,且△ABO的面积为16,过A′作A′C′⊥x′轴,则A′C′的长为( )
如图是利用斜二测画法画出的△ABO的直观图,已知O′B′=4,且△ABO的面积为16,过A′作A′C′⊥x′轴,则A′C′的长为( )| A. | $2\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $16\sqrt{2}$ | D. | 1 |
17.已知某几何体的三视图如图所示,其中俯视图是扇形,则该几何体的体积为( )
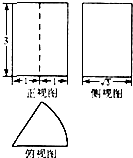

| A. | 4 π | B. | 2 π | C. | $\frac{4π}{3}$ | D. | $\frac{2π}{3}$ |