题目内容
20．某观察站C与两灯塔A、B的距离分别为300米和500米，测得灯塔A在观察站C北偏东30°，灯塔B在观察站C南偏东30°处，则两灯塔A、B间的距离为700米．分析 根据题意，△ABC中，AC=300米，BC=500米，∠ACB=120°，利用余弦定理可求得AB的长
解答 解：由题意，如图，△ABC中，AC=300米，BC=500米，∠ACB=120°，
利用余弦定理可得：AB2=3002+5002-2×300×500×cos120°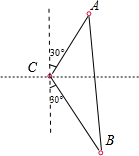
，
∴AB=700米，
故答案为：700米．
点评 本题以方位角为载体，考查三角形的构建，余弦定理的运用，属于中档题．
练习册系列答案
相关题目
10．已知函数f（x）=$\frac{{e}^{x}+m}{{e}^{x}+1}$，若对?a，b，c∈R，都有f（a）+f（b）＞f（c）成立，则实数m的取值范围是[$\frac{1}{2}$，2]．
11．如图所示的是一串黑白相间排列的珠子，若按这种规律排列下去，那么第36颗珠子的颜色是 （ ）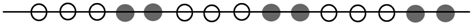
| A． | 白色 | B． | 黑色 | C． | 白色的可能性大 | D． | 黑色的可能性大 |
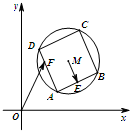如图，已知圆M：（x-3）2+（y-3）2=4，四边形ABCD为圆M的内接正方形，E为边AB的中点，当正方形ABCD绕圆心M转动，同时点F在边AD上运动时，$\overrightarrow{ME}$$•\overrightarrow{OF}$的最大值是8．