题目内容
19.在△ABC中,角A,B,C的对边分别为a,b,c,向量$\overrightarrow{m}$=(1-sin$\frac{C}{2}$,-1),$\overrightarrow{n}$=(1,sinC+cosC),且$\overrightarrow{m}$⊥$\overrightarrow{n}$(1)求sinC的值;
(2)若a2+b2=4(a+b)-8,求边c的长度.
分析 (1)利用量向量垂直得出结论$\overrightarrow{m}$•$\overrightarrow{n}$=0,代入坐标整理可求得sinC.
(2)把原等式整理成(a-2)2+(b-2)2=0,求得a和b,根据sinC求得cosC,进而利用余弦定理求得c.
解答 解:(1)∵$\overrightarrow{m}$⊥$\overrightarrow{n}$
,∴$\overrightarrow{m}$•$\overrightarrow{n}$=0,则1-sin$\frac{C}{2}$-(sinC+cosC)=0,
即1-sin$\frac{C}{2}$=2sin$\frac{C}{2}$cos$\frac{C}{2}$+1-2sin2$\frac{C}{2}$(*),
又$\frac{C}{2}$∈(0,$\frac{π}{2}$),
∴sin$\frac{C}{2}$∈(0,1),
故(*)可化简为cos$\frac{C}{2}$-sin$\frac{C}{2}$=-$\frac{1}{2}$,两边平方得
1-sinC=$\frac{1}{4}$,
∴sinC=$\frac{3}{4}$.
(2)又a2+b2=4(a+b)-8得(a-2)2+(b-2)2=0,
∴a=2,b=2,
由(1)知cos$\frac{C}{2}$-sin$\frac{C}{2}$=-$\frac{1}{2}$<0,
∴$\frac{C}{2}$∈($\frac{π}{4}$,$\frac{π}{2}$),c∈($\frac{π}{2}$,π),
∴cosC=-$\frac{-\sqrt{7}}{4}$,
∴在△ABC中,由余弦定理可得c2=a2+b2-2abcosC=4+4-2×2×2×(-$\frac{\sqrt{7}}{4}$)=8+2$\sqrt{7}$,
故c=$\sqrt{7}$+1.
点评 本题主要考查了余弦定理的应用.注重了对学生推理能力和解题能力的考查.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
| A. | {0,4,5,2} | B. | {0,4,5} | C. | {4,5,2} | D. | {4,5} |
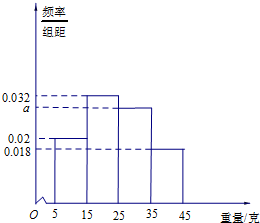 测量马口鱼性成熟时重量,从大量马口鱼中随机抽取100尾作为样本,测出它们的重量(单位:克),重量分组区间为(5,15],(15,25],(25,35],(35,45],由此得到重量样本的频率分布直方图,如图.
测量马口鱼性成熟时重量,从大量马口鱼中随机抽取100尾作为样本,测出它们的重量(单位:克),重量分组区间为(5,15],(15,25],(25,35],(35,45],由此得到重量样本的频率分布直方图,如图. 一个由若干行数字组成的数表,从第二行起,每一行中的数字均等于其肩上两个数字之和,最后一行仅有一个数,第一行是前100个正整数按从小到大排成的行,则最后一行的数是101×298.
一个由若干行数字组成的数表,从第二行起,每一行中的数字均等于其肩上两个数字之和,最后一行仅有一个数,第一行是前100个正整数按从小到大排成的行,则最后一行的数是101×298.