题目内容
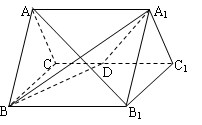
在直三棱柱 中,
中, ,直线
,直线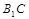 与平面
与平面 成30°角.
成30°角.
(I)求证:平面 平面
平面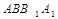 ;
;
(II)求直线 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(III)求二面角 的平面角的余弦值.
的平面角的余弦值.

 中,
中, ,直线
,直线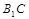 与平面
与平面 成30°角.
成30°角.(I)求证:平面
 平面
平面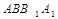 ;
;(II)求直线
 与平面
与平面 所成角的正弦值;
所成角的正弦值;(III)求二面角
 的平面角的余弦值.
的平面角的余弦值.
(1)见解析;(2)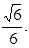 (3)
(3)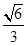 .
.
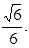 (3)
(3)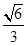 .
.本试题主要考查了空间想象能力的运用,解决空间中的线面角二面角以及面面垂直的判定定理的运用。
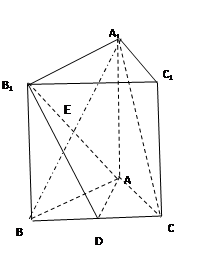
(1)证明:由直三棱柱性质,B1B⊥平面ABC,
∴B1B⊥AC,
又BA⊥AC,B1B∩BA=B,
∴AC⊥平面 ABB1A1,
又AC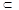 平面B1AC,
平面B1AC,
∴平面B1AC⊥平面ABB1A1.
(2)解:过A1做A1M⊥B1A1,垂足为M,连结CM,
∵平面B1AC⊥平面ABB1A,且平面B1AC∩平面ABB1A1=B1A,
∴A1M⊥平面B1AC.
∴∠A1CM为直线A1C与平面B1AC所成的角,
∵直线B1C与平面ABC成30°角,
∴∠B1CB=30°.
设AB=BB1=a,可得B1C=2a,BC=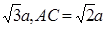 ,
,
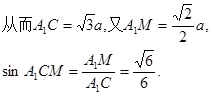
∴直线A1C与平面B1AC所成角的正弦值为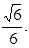
(3)解:过A做AN⊥BC,垂足为N,过N做NO⊥B1C,垂足为O,连结AO,
由AN⊥BC,可得AN⊥平面BCC1B1,由三垂线定理,可知AO⊥B1C,
∴∠AON为二面角B—B1C—A的平面角,
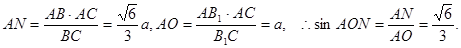
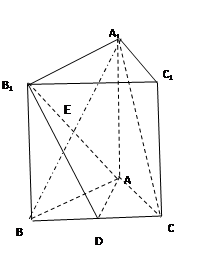
(1)证明:由直三棱柱性质,B1B⊥平面ABC,
∴B1B⊥AC,
又BA⊥AC,B1B∩BA=B,
∴AC⊥平面 ABB1A1,
又AC
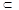 平面B1AC,
平面B1AC,∴平面B1AC⊥平面ABB1A1.
(2)解:过A1做A1M⊥B1A1,垂足为M,连结CM,
∵平面B1AC⊥平面ABB1A,且平面B1AC∩平面ABB1A1=B1A,
∴A1M⊥平面B1AC.
∴∠A1CM为直线A1C与平面B1AC所成的角,
∵直线B1C与平面ABC成30°角,
∴∠B1CB=30°.
设AB=BB1=a,可得B1C=2a,BC=
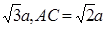 ,
,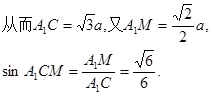
∴直线A1C与平面B1AC所成角的正弦值为
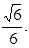
(3)解:过A做AN⊥BC,垂足为N,过N做NO⊥B1C,垂足为O,连结AO,
由AN⊥BC,可得AN⊥平面BCC1B1,由三垂线定理,可知AO⊥B1C,
∴∠AON为二面角B—B1C—A的平面角,
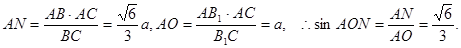

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
 和正
和正
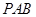 所在平面互相垂直,其中
所在平面互相垂直,其中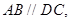
 ,且
,且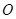 为
为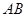 中点.
中点. 
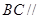 平面
平面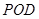 ;
;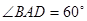 ,求二面角
,求二面角 的余弦值;
的余弦值;
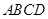 中,已知
中,已知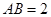 ,
,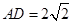 ,
, 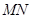 分别为
分别为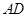 和
和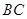 的中点,对角线
的中点,对角线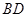 与
与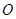 点,沿
点,沿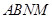 折起,使平面
折起,使平面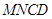 所成角为
所成角为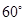 ,如图5(2).
,如图5(2).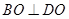 ;
;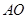 与平面
与平面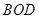 所成角的正弦值.
所成角的正弦值.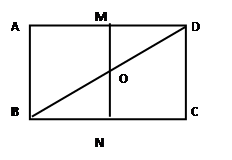

 平面
平面 ,点P
,点P
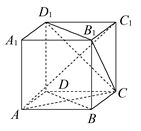
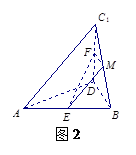
 (如图1所示),将菱形ABCD沿对角线
(如图1所示),将菱形ABCD沿对角线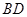 翻折,使点
翻折,使点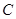 翻折到点
翻折到点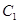 的位置(如图2所示),点E,F,M分别是AB,DC1,BC1的中点.
的位置(如图2所示),点E,F,M分别是AB,DC1,BC1的中点.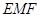 ;
;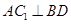 ;
;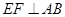 时,求线段AC1的长.
时,求线段AC1的长.
 表示平面,m,n表示直线,则m//
表示平面,m,n表示直线,则m// 的一个充分条件是( )
的一个充分条件是( ) 



 的所有棱长都为2,
的所有棱长都为2, 为棱
为棱 的中点,
的中点, 平面
平面 ;
; 的余弦值大小.
的余弦值大小.