题目内容
如图5(1)中矩形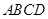 中,已知
中,已知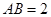 ,
,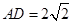 ,
, 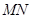 分别为
分别为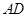 和
和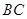 的中点,对角线
的中点,对角线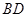 与
与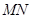 交于
交于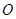 点,沿
点,沿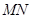 把矩形
把矩形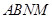 折起,使平面
折起,使平面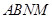 与平面
与平面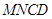 所成角为
所成角为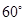 ,如图5(2).
,如图5(2).
(1) 求证: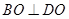 ;
;
(2) 求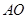 与平面
与平面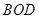 所成角的正弦值.
所成角的正弦值.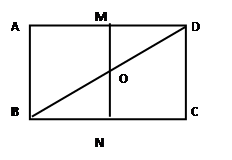

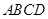 中,已知
中,已知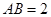 ,
,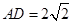 ,
, 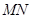 分别为
分别为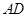 和
和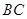 的中点,对角线
的中点,对角线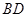 与
与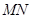 交于
交于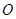 点,沿
点,沿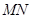 把矩形
把矩形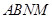 折起,使平面
折起,使平面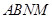 与平面
与平面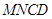 所成角为
所成角为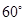 ,如图5(2).
,如图5(2).(1) 求证:
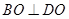 ;
;(2) 求
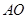 与平面
与平面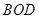 所成角的正弦值.
所成角的正弦值.

(1)见解析;(2) .
.
 .
.本试题主要是考查了立体几何中的线线垂直的判定和线面所成角的正弦值的运用。
解:(1)由题设,M,N是矩形的边AD和BC的中点,所以AM MN, BC
MN, BC MN, 折叠垂直关系不变,所以∠AMD 是平面ABMN与平面MNCD的平面角,依题意,所以∠AMD=60o,……2分
MN, 折叠垂直关系不变,所以∠AMD 是平面ABMN与平面MNCD的平面角,依题意,所以∠AMD=60o,……2分
由AM=DM,可知△MAD是正三角形,所以AD=,在矩形ABCD中,AB=2,AD= ,所以,BD=
,所以,BD= ,由题可知BO=OD=
,由题可知BO=OD= ,由勾股定理可知三角形BOD是直角三角形,所以BO⊥DO
,由勾股定理可知三角形BOD是直角三角形,所以BO⊥DO
…………5分
解(2)设E,F是BD,CD的中点,则EF CD, OF
CD, OF CD, 所以,CD
CD, 所以,CD 面OEF, OE
面OEF, OE CD
CD
又BO=OD,所以OE BD, OE
BD, OE 面ABCD, OE
面ABCD, OE 面BOD, 平面BOD⊥平面ABCD
面BOD, 平面BOD⊥平面ABCD
过A作AH⊥BD,由面面垂直的性质定理,可得AH⊥平面BOD,连结OH ,…………… 8分

所以OH是AO在平面BOD的投影,所以∠AOH为所求的角,即AO与平面BOD所成角。11分
AH是RT△ABD斜边上的高,所以AH= ,BO=OD=
,BO=OD= ,
,
所以sin∠AOH= (14分)
(14分)
方法二:空间向量:取MD,NC中点P,Q,如图建系,

Q(0,0,0),B( ,0,0),D(0,
,0,0),D(0, ,2),O(0,
,2),O(0, ,1
,1
所以 (
( ,
, ,1),
,1), (0,
(0, ,
,
所以
 0,即BO⊥DO(5分)
0,即BO⊥DO(5分)
(2)设平面BOD的法向量是 ,可得
,可得 x
x y+z=0
y+z=0
 y-z=0,令
y-z=0,令 可得
可得 所以
所以
又 (
( ,
, ,-1),
,-1),
设AO与平面BOD所成角为 ,jsin
,jsin =|cos<
=|cos< >|==
>|== (14分)
(14分)
解:(1)由题设,M,N是矩形的边AD和BC的中点,所以AM
 MN, BC
MN, BC MN, 折叠垂直关系不变,所以∠AMD 是平面ABMN与平面MNCD的平面角,依题意,所以∠AMD=60o,……2分
MN, 折叠垂直关系不变,所以∠AMD 是平面ABMN与平面MNCD的平面角,依题意,所以∠AMD=60o,……2分由AM=DM,可知△MAD是正三角形,所以AD=,在矩形ABCD中,AB=2,AD=
 ,所以,BD=
,所以,BD= ,由题可知BO=OD=
,由题可知BO=OD= ,由勾股定理可知三角形BOD是直角三角形,所以BO⊥DO
,由勾股定理可知三角形BOD是直角三角形,所以BO⊥DO…………5分
解(2)设E,F是BD,CD的中点,则EF
 CD, OF
CD, OF CD, 所以,CD
CD, 所以,CD 面OEF, OE
面OEF, OE CD
CD又BO=OD,所以OE
 BD, OE
BD, OE 面ABCD, OE
面ABCD, OE 面BOD, 平面BOD⊥平面ABCD
面BOD, 平面BOD⊥平面ABCD过A作AH⊥BD,由面面垂直的性质定理,可得AH⊥平面BOD,连结OH ,…………… 8分

所以OH是AO在平面BOD的投影,所以∠AOH为所求的角,即AO与平面BOD所成角。11分
AH是RT△ABD斜边上的高,所以AH=
 ,BO=OD=
,BO=OD= ,
,所以sin∠AOH=
 (14分)
(14分)方法二:空间向量:取MD,NC中点P,Q,如图建系,

Q(0,0,0),B(
 ,0,0),D(0,
,0,0),D(0, ,2),O(0,
,2),O(0, ,1
,1所以
 (
( ,
, ,1),
,1), (0,
(0, ,
,
所以

 0,即BO⊥DO(5分)
0,即BO⊥DO(5分)(2)设平面BOD的法向量是
 ,可得
,可得 x
x y+z=0
y+z=0 y-z=0,令
y-z=0,令 可得
可得 所以
所以
又
 (
( ,
, ,-1),
,-1),设AO与平面BOD所成角为
 ,jsin
,jsin =|cos<
=|cos< >|==
>|== (14分)
(14分)
练习册系列答案
相关题目
 中,
中, ,直线
,直线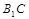 与平面
与平面 成30°角.
成30°角. 平面
平面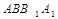 ;
; 与平面
与平面 所成角的正弦值;
所成角的正弦值; 的平面角的余弦值.
的平面角的余弦值.
 、
、 、
、 和直线
和直线 、
、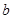 、m、n,下列命题中真命题是
、m、n,下列命题中真命题是 ,则
,则
 ,则
,则
 ,则
,则
 则
则
 为两条不同的直线,
为两条不同的直线,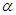 、
、 为两个不同的平面,则下列命题正确的是
为两个不同的平面,则下列命题正确的是 ;
;


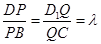 .
. 的值.
的值.
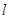 ,
,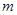 是两条不同的直线,
是两条不同的直线,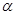 是一个平面,则下列命题正确的是( )
是一个平面,则下列命题正确的是( ) ,
, ,则
,则
 ,则
,则
 ,
, ,则
,则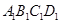 中,平面
中,平面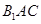 与面
与面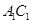 的交线为l,则l与AC的关系是( )。
的交线为l,则l与AC的关系是( )。 ,将
,将 沿AB折到
沿AB折到 的位置,使
的位置,使 ,点E在SD上,且
,点E在SD上,且 ,如下右图。
,如下右图。 平面ABCD;(2)求二面角E—AC—D的正切值.
平面ABCD;(2)求二面角E—AC—D的正切值.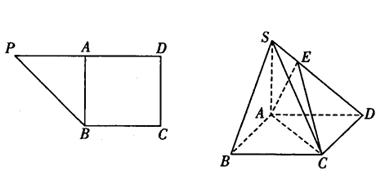
 、
、 ,平面
,平面 ,则下列命题中假命题是
,则下列命题中假命题是 ,
, ,则
,则
 ,则
,则
 ,
, ,则
,则
 ,
, ,
, ,则
,则