题目内容
(本题满分10分)
如图,已知正三棱柱 的所有棱长都为2,
的所有棱长都为2, 为棱
为棱 的中点,
的中点,
(1)求证: 平面
平面 ;
;
(2)求二面角 的余弦值大小.
的余弦值大小.
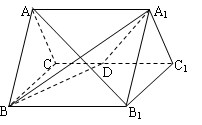
如图,已知正三棱柱
 的所有棱长都为2,
的所有棱长都为2, 为棱
为棱 的中点,
的中点,(1)求证:
 平面
平面 ;
;(2)求二面角
 的余弦值大小.
的余弦值大小.
(本题满分10分)
(1)取 中点
中点 ,连
,连 ,∵
,∵ 为正三角形,∴
为正三角形,∴ ,
,
∵在正三棱柱 中,平面
中,平面
 平面
平面 ,∴
,∴ 平面
平面 ………2分
………2分
取 中点为
中点为 ,以
,以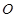 为原点,
为原点, ,
,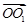 ,
,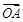 的方向为
的方向为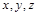 轴的正方向,建立空间直角坐标系,则
轴的正方向,建立空间直角坐标系,则 ,
,

 ……………4分
……………4分
∴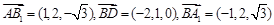 ,
,
∵ ,
, ,
,
∴ ,
, ,
,
∴ 平面
平面 . ……………………………6分
. ……………………………6分
(2)设平面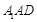 的法向量为
的法向量为 ,
, .
.
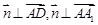 ,∴
,∴ ,∴
,∴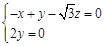 ,解得
,解得 ,
,
令 ,得
,得 为平面
为平面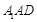 的一个法向量, ………………………8分
的一个法向量, ………………………8分
由(1)知 平面
平面 ,∴
,∴ 为平面
为平面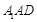 的法向量,
的法向量,
 ,
,
∴二面角 的余弦值大小为
的余弦值大小为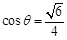 . ……………………10分
. ……………………10分
(1)取
 中点
中点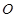 ,连
,连 ,∵
,∵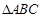 为正三角形,∴
为正三角形,∴ ,
,∵在正三棱柱
 中,平面
中,平面
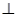 平面
平面 ,∴
,∴ 平面
平面 ………2分
………2分取
 中点为
中点为 ,以
,以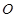 为原点,
为原点, ,
,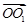 ,
,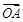 的方向为
的方向为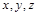 轴的正方向,建立空间直角坐标系,则
轴的正方向,建立空间直角坐标系,则 ,
,
 ……………4分
……………4分∴
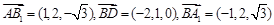 ,
,∵
 ,
, ,
,∴
 ,
, ,
,∴
 平面
平面 . ……………………………6分
. ……………………………6分(2)设平面
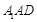 的法向量为
的法向量为 ,
, .
.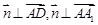 ,∴
,∴ ,∴
,∴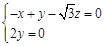 ,解得
,解得 ,
,令
 ,得
,得 为平面
为平面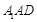 的一个法向量, ………………………8分
的一个法向量, ………………………8分由(1)知
 平面
平面 ,∴
,∴ 为平面
为平面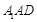 的法向量,
的法向量, ,
,∴二面角
 的余弦值大小为
的余弦值大小为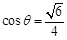 . ……………………10分
. ……………………10分略

练习册系列答案
相关题目
 中,
中, ,直线
,直线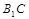 与平面
与平面 成30°角.
成30°角. 平面
平面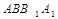 ;
; 与平面
与平面 所成角的正弦值;
所成角的正弦值; 的平面角的余弦值.
的平面角的余弦值.
 .
.
 ,EF =
,EF =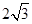 ,则另一边BC的长为何值时,二面角B-EF-D的大小为45°?
,则另一边BC的长为何值时,二面角B-EF-D的大小为45°? 是互不重合的平面,给出下列命题:( )
是互不重合的平面,给出下列命题:( ) ;
; ;
;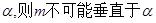 内的无数条直线;
内的无数条直线; .
. 、
、 ,平面
,平面 ,则下列命题中假命题是
,则下列命题中假命题是 ,
, ,则
,则
 ,则
,则
 ,
, ,则
,则
 ,
, ,
, ,则
,则
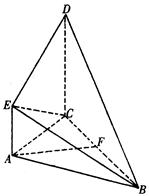
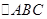 所在平面互相垂直,F为BC的中点,
所在平面互相垂直,F为BC的中点,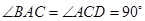 ,AE∥CD,
,AE∥CD,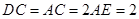 .
.
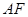 ∥平面
∥平面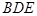 ;
;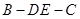 的余弦值.
的余弦值. ,直线
,直线 平面
平面 ,有下列四个命题:①
,有下列四个命题:① ,②
,② l∥m,③l∥m
l∥m,③l∥m ,④
,④
 ∥
∥