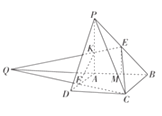
题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过其右焦点F且与x轴垂直的直线交椭圆C于P,Q两点,椭圆C的右顶点为R,且满足
,过其右焦点F且与x轴垂直的直线交椭圆C于P,Q两点,椭圆C的右顶点为R,且满足![]() .
.

(1)求椭圆C的方程;
(2)若斜率为k(其中![]() )的直线l过点F,且与椭圆交于点A,B,弦AB的中点为M,直线OM与椭圆交于点C,D,求四边形ACBD面积
)的直线l过点F,且与椭圆交于点A,B,弦AB的中点为M,直线OM与椭圆交于点C,D,求四边形ACBD面积![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)(6,
;(2)(6,![]() ) .
) .
【解析】
(1)根据离心率及![]() ,结合椭圆的定义即可求得椭圆的方程。
,结合椭圆的定义即可求得椭圆的方程。
(2)设出直线方程,联立椭圆方程化简即可得关于x的一元二次方程,根据韦达定理即可得AB的表达式,然后求得点![]() 到直线
到直线![]() 的距离之和为
的距离之和为![]() ,进而表达出四边形ACBD面积
,进而表达出四边形ACBD面积![]() ,即可求得S的取值范围。
,即可求得S的取值范围。
(1)由![]() 得
得![]()
![]() =2(a-c)=2
=2(a-c)=2
∴![]() ,
,![]()
∴椭圆![]() 。
。
(2)由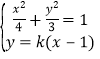 消y得
消y得![]()
∴Δ=122(k2+1)恒正,![]() ,
,![]()
∴![]() =
=![]() ,
,
M(![]() ,-
,-![]() ) ∴kOM=-
) ∴kOM=-![]()
(此处也可以用点差法:由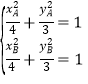 得
得![]()
∴![]() ,∴kOM=
,∴kOM=![]() =-
=-![]() )
)
由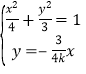 得
得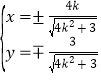 ,即为C、D两点的坐标,
,即为C、D两点的坐标,
∴点![]() 到直线
到直线![]() 的距离之和为
的距离之和为![]()
![]() =2
=2![]() ,
,
∴S![]() =
=![]() ×
×![]() ×2
×2![]()
=![]() (k≠0),
(k≠0),
∴S的取值范围=(6,![]() ).
).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目