题目内容
(Ⅰ) 以直角坐标系的原点为极点,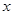 轴的正半轴为极轴,并在两种坐标系中取相同的长度单位已知直线的极坐标方程为
轴的正半轴为极轴,并在两种坐标系中取相同的长度单位已知直线的极坐标方程为 ,它与曲线
,它与曲线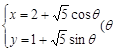 为参数)相交于两点A和B, 求|AB|;
为参数)相交于两点A和B, 求|AB|;
(Ⅱ)已知极点与原点重合,极轴与x轴正半轴重合,若直线C1的极坐标方程为: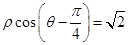 ,曲线C2的参数方程为:
,曲线C2的参数方程为: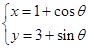 (
(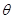 为参数),试求曲线C2关于直线C1对称的曲线的直角坐标方程
为参数),试求曲线C2关于直线C1对称的曲线的直角坐标方程
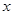 轴的正半轴为极轴,并在两种坐标系中取相同的长度单位已知直线的极坐标方程为
轴的正半轴为极轴,并在两种坐标系中取相同的长度单位已知直线的极坐标方程为 ,它与曲线
,它与曲线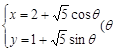 为参数)相交于两点A和B, 求|AB|;
为参数)相交于两点A和B, 求|AB|; (Ⅱ)已知极点与原点重合,极轴与x轴正半轴重合,若直线C1的极坐标方程为:
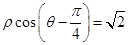 ,曲线C2的参数方程为:
,曲线C2的参数方程为: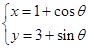 (
(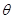 为参数),试求曲线C2关于直线C1对称的曲线的直角坐标方程
为参数),试求曲线C2关于直线C1对称的曲线的直角坐标方程(Ι)|AB|= (Ⅱ)
(Ⅱ)
 (Ⅱ)
(Ⅱ)
(I)先把直线和圆的方程化成普通方程,求出圆心坐标,再求出圆心到直线的距离d,利用弦长公式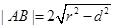 求解即可.
求解即可.
先把两曲线的极坐标方程化成普通方程,然后求出圆C2的圆心关于直线C1的对称点,半径不变,可求出对称曲线的方程.
(2)解:(Ι)直线和圆的直角坐标方程分别为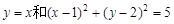 …………1分
…………1分
则圆心为C(1,2),半径R=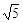 ,………………2分
,………………2分
从而C到直线y=x的距离d=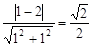 ……………………3分
……………………3分
由垂径定理得,|AB|= ……………4分
……………4分
(Ⅱ)曲线C1可化为: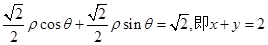 ………5分
………5分
曲线C2是以(1,3)为圆心,1为半径的圆………………6分
(1,3)关于直线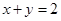 的对称点(-1,1)故所求曲线为圆
的对称点(-1,1)故所求曲线为圆
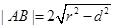 求解即可.
求解即可.先把两曲线的极坐标方程化成普通方程,然后求出圆C2的圆心关于直线C1的对称点,半径不变,可求出对称曲线的方程.
(2)解:(Ι)直线和圆的直角坐标方程分别为
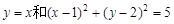 …………1分
…………1分则圆心为C(1,2),半径R=
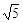 ,………………2分
,………………2分从而C到直线y=x的距离d=
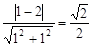 ……………………3分
……………………3分由垂径定理得,|AB|=
 ……………4分
……………4分(Ⅱ)曲线C1可化为:
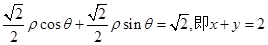 ………5分
………5分曲线C2是以(1,3)为圆心,1为半径的圆………………6分
(1,3)关于直线
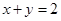 的对称点(-1,1)故所求曲线为圆
的对称点(-1,1)故所求曲线为圆

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
 (θ为参数)
(θ为参数) (t为参数)
(t为参数)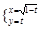 (t为参数)
(t为参数)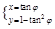 (φ为参数)
(φ为参数)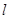 经过点
经过点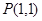 ,倾斜角
,倾斜角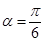 ,
,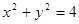 相交与两点A,B.求点P到A、B两点的距离的和与积.
相交与两点A,B.求点P到A、B两点的距离的和与积. 的参数方程为
的参数方程为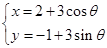 (
(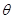 为参数),直线
为参数),直线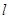 的方程为
的方程为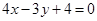 ,则曲线
,则曲线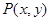 到直线
到直线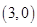 到直线
到直线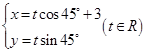 与直线
与直线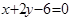 的交点Q的距离为
的交点Q的距离为  (t为参数)上对应t="0," t=1两点间的距离是___________.
(t为参数)上对应t="0," t=1两点间的距离是___________.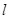 :
: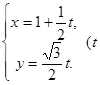 为参数), 曲线
为参数), 曲线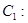
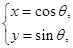 (
(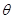 为参数).
为参数).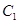 相交于
相交于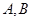 两点,求
两点,求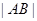 ;
;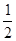 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的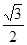 倍,得到曲线
倍,得到曲线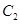 ,设点
,设点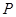 是曲线
是曲线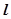 的距离的最小值.
的距离的最小值. 的参数方程是
的参数方程是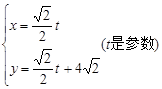 ,圆C的极坐标方程为
,圆C的极坐标方程为 .
.