题目内容
【题目】已知![]() .
.
(1)若x,![]() ,求
,求![]() ,
,![]() 的值;
的值;
(2)若x,![]() ,试判断
,试判断![]() 的奇偶性;
的奇偶性;
(3)若函数![]() 在其定义域
在其定义域![]() 上是增函数,
上是增函数,![]() ,
,![]() ,求实数的取值范围.
,求实数的取值范围.
【答案】(1)f(1)=0,f(![]() 1)=0(2)见解析(3){x|2<x≤4}
1)=0(2)见解析(3){x|2<x≤4}
【解析】
(1)利用已知条件,通过赋值法即可f(1),f(﹣1)的值;
(2)通过(1)f(﹣1)=0,利用函数的奇偶性定义,判断y=f(x)的奇偶性;
(3)利用函数f(x)在其定义域(0,+∞)上是增函数,结合f(2)=1,f(x)+f(x﹣2)≤3,得到不等式组,即可求x的取值范围.
解;(1)令x=y=1,则f(1)=f(1)+f(1),所以f(1)=0;
又令x=y=﹣1,则f(1)=f(﹣1)+f(﹣1),所以f(﹣1)=0;
(2)令y=﹣1,则f(﹣x)=f(x)+f(﹣1),由(1)知f(﹣1)=0
所以f(﹣x)=f(x),即函数f(x)为偶函数,
(3)因为f(4)=f(2)+f(2)=1+1=2
所以f(8)=f(2)+f(4)=1+2=3
因为f(x)+f(x﹣2)≤3
所以f[x(x﹣2)]≤f(8)
因为f(x)在(0,+∞)上是增函数
所以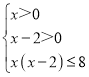 ,即
,即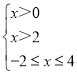
所以{x|2<x≤4},所以不等式的解集为{x|2<x≤4}

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】在考察黄烟经过药物处理和发生青花病的关系时,得到如下数据:在试验的470株黄烟中,经过药物处理的黄烟有25株发生青花病,60株没有发生青花病;未经过药物处理的有185株发生青花病,200株没有发生青花病.试推断药物处理跟发生青花病是否有关系.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |


