题目内容
【题目】已知椭圆![]() 以
以![]() ,
,![]() 为左右焦点,且与直线
为左右焦点,且与直线![]() :
:![]() 相切于点
相切于点![]() .
.

(1)求椭圆的方程及点![]() 的坐标;
的坐标;
(2)若直线![]() :
:![]() 与椭圆交于
与椭圆交于![]() 两点,且
两点,且![]() 交
交![]() 于点
于点![]() (异于点
(异于点![]() ),求证:线段长
),求证:线段长![]() ,
,![]() ,
,![]() 成等比数列.
成等比数列.
【答案】(1) ![]()
![]() (2)见解析
(2)见解析
【解析】
(1) 设椭圆方程为![]()
![]() ,联立椭圆和直线
,联立椭圆和直线![]() 的方程可得
的方程可得![]() ,由相切条件可得
,由相切条件可得![]() ,从而得到椭圆的方程及点
,从而得到椭圆的方程及点![]() 的坐标;
的坐标;
(2) 联立直线![]() 与
与![]() 的方程解得
的方程解得![]() 点为
点为![]() ,由弦长公式
,由弦长公式![]() ,联立椭圆与直线
,联立椭圆与直线![]() 的方程,消去
的方程,消去![]() 得
得![]() ,可得
,可得![]() ,
,
![]()
![]() ,从而可证线段长
,从而可证线段长![]() ,
,![]() ,
,![]() 成等比数列.
成等比数列.
(1)由题意,设椭圆方程为![]()
![]() ,联立椭圆和直线
,联立椭圆和直线![]() 的方程
的方程
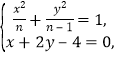 消去
消去![]() 得
得![]()
所以![]()
![]() ,
,
化简得![]() ,由
,由![]() 知,
知,![]() ,所以椭圆方程为
,所以椭圆方程为![]() .
.
将![]() 代回原方程组,解得切点
代回原方程组,解得切点![]() 的坐标为
的坐标为![]() .
.
(2)联立直线![]() 与
与![]() 的方程
的方程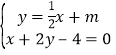 解得
解得![]() 点为
点为![]() ,
,
又因为![]() ,
,
由弦长公式![]()
![]()
![]() 得,所以
得,所以![]() .
.
设![]() ,
,![]() ,联立椭圆与直线
,联立椭圆与直线![]() 的方程,
的方程,
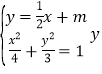 ,消去
,消去![]() 得
得![]() ,
,
![]()
![]() ,得
,得![]()
则![]() ,
,![]()
又因为![]()
![]() ,
,
![]()
![]()
![]() ,
,
所以![]()
![]()
![]()
![]()
![]()
![]()
所以线段长![]() ,
,![]() ,
,![]() 成等比数列.
成等比数列.

【题目】随着电商的快速发展,快递业突飞猛进,到目前,中国拥有世界上最大的快递市场.某快递公司收取快递费用的标准是:重量不超过![]() 的包裹收费10元;重量超过
的包裹收费10元;重量超过![]() 的包裹,除
的包裹,除![]() 收费10元之外,每超过
收费10元之外,每超过![]() (不足
(不足![]() ,按
,按![]() 计算)需再收5元.
计算)需再收5元.
该公司将最近承揽的100件包裹的重量统计如下:
包裹重量(单位: | 1 | 2 | 3 | 4 | 5 |
包裹件数 | 43 | 30 | 15 | 8 | 4 |
公司对近60天,每天揽件数量统计如下表:
包裹件数范围 | 0~100 | 101~200 | 201~300 | 301~400 | 401~500 |
包裹件数(近似处理) | 50 | 150 | 250 | 350 | 450 |
天数 | 6 | 6 | 30 | 12 | 6 |
以上数据已做近似处理,并将频率视为概率.
(1)计算该公司未来5天内恰有2天揽件数在101~300之间的概率;
(2)①估计该公司对每件包裹收取的快递费的平均值;
②根据以往的经验,公司将快递费的三分之一作为前台工作人员的工资和公司利润,剩余的用作其他费用.目前前台有工作人员3人,每人每件揽件不超过150件,日工资100元.公司正在考虑是否将前台工作人员裁减1人,试计算裁员前后公司每日利润的数学期望,若你是公司老总,是否进行裁减工作人员1人?




